Mixed effect Models

Bio300B Lecture 10

Richard J. Telford (Richard.Telford@uib.no)

Institutt for biovitenskap, UiB

30 October 2023

Assumptions of Least Squares

  1. Linear relationship between response and predictors.
  2. The residuals have a mean of zero.
  3. The residuals have constant variance (not heteroscedastic).
  4. The residuals are independent (uncorrelated).
  5. The residuals are normally distributed.
  • Spatial/temporal/phylogenetic autocorrelation
  • Clustered/hierarchical data

Clustered data

Observations not independent

  • clustered data
  • repeat measurements

Ignoring it causes pseudoreplication

Two tanks - bad design

Two tanks - bad models

mod_bad <- lm(Mass_g ~ condition, data = demo)
mod_bad2 <- lm(Mass_g ~ tank, data = demo)

mod_bad

Call:
lm(formula = Mass_g ~ condition, data = demo)

Coefficients:
  (Intercept)  conditiontest  
       1147.6         -105.1  
mod_bad2

Call:
lm(formula = Mass_g ~ tank, data = demo)

Coefficients:
(Intercept)    tanktank2  
     1147.6       -105.1

Better design - replicate tanks

Better design, bit better model

mod_bit <- lm(Mass_g ~ condition + tank, data = demo2)
summary(mod_bit)

Call:
lm(formula = Mass_g ~ condition + tank, data = demo2)

Residuals:
    Min      1Q  Median      3Q     Max 
-270.11  -59.70   20.80   71.17  224.67 

Coefficients: (1 not defined because of singularities)
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)    1202.37      33.38  36.021  < 2e-16 ***
conditiontest   -68.44      47.21  -1.450 0.151439    
tanktank2      -118.07      47.21  -2.501 0.014654 *  
tanktank3      -195.25      47.21  -4.136 9.44e-05 ***
tanktank4        33.35      47.21   0.707 0.482102    
tanktank5      -178.79      47.21  -3.788 0.000313 ***
tanktank6       -49.47      47.21  -1.048 0.298128    
tanktank7       -96.71      47.21  -2.049 0.044128 *  
tanktank8           NA         NA      NA       NA    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 105.6 on 72 degrees of freedom
Multiple R-squared:  0.3187,    Adjusted R-squared:  0.2525 
F-statistic: 4.812 on 7 and 72 DF,  p-value: 0.0001745

Fixed effect and random effects

Fixed effect effect model

\[y_i = \color{red}{\beta_0} + \color{red}{\beta_1}x_i + \color{red}{\beta_2}tank_i +\color{blue}{ \epsilon_i}\]

Not interested in effect of tank

Mixed effect model

Use a Random effect

Assumes observed tanks from a population of possible tanks

\[y_{ij} = \color{red}{\beta_0} +\color{blue}{b_{0i}}+ \color{red}{\beta_1}x_i +\color{blue}{ \epsilon_{ij}}\]

Random effects

Residuals from a normal distribution \(\color{blue}{ \epsilon_{ij}} \sim N(0, \sigma_{ind})\)
Random effects from a normal distribution \(\color{blue}{b_{0i}} \sim N(0, \sigma_{clu})\)

Fitting a mixed effect model

library(lme4)
mod1 <- lmer(Mass_g ~ condition + (1|tank), data = demo2)
summary(mod1)
Linear mixed model fit by REML ['lmerMod']
Formula: Mass_g ~ condition + (1 | tank)
   Data: demo2

REML criterion at convergence: 965.8

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.6916 -0.5419  0.1989  0.6274  2.2428 

Random effects:
 Groups   Name        Variance Std.Dev.
 tank     (Intercept)  5059     71.13  
 Residual             11142    105.56  
Number of obs: 80, groups:  tank, 8

Fixed effects:
              Estimate Std. Error t value
(Intercept)    1084.68      39.28  27.611
conditiontest    15.70      55.56   0.283

Correlation of Fixed Effects:
            (Intr)
conditintst -0.707
library(lmerTest)
mod1a <- lmer(Mass_g ~ condition + (1|tank), data = demo2)
summary(mod1a)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Mass_g ~ condition + (1 | tank)
   Data: demo2

REML criterion at convergence: 965.8

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.6916 -0.5419  0.1989  0.6274  2.2428 

Random effects:
 Groups   Name        Variance Std.Dev.
 tank     (Intercept)  5059     71.13  
 Residual             11142    105.56  
Number of obs: 80, groups:  tank, 8

Fixed effects:
              Estimate Std. Error      df t value Pr(>|t|)    
(Intercept)    1084.68      39.28    6.00  27.611 1.49e-07 ***
conditiontest    15.70      55.56    6.00   0.283    0.787    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr)
conditintst -0.707

Alternative package

library(nlme)
mod2 <- lme(Mass_g ~ condition, data = demo2, random =  ~ 1|tank)
summary(mod2)
Linear mixed-effects model fit by REML
  Data: demo2 
       AIC      BIC    logLik
  973.8449 983.2717 -482.9225

Random effects:
 Formula: ~1 | tank
        (Intercept) Residual
StdDev:    71.12618  105.555

Fixed effects:  Mass_g ~ condition 
                  Value Std.Error DF   t-value p-value
(Intercept)   1084.6791  39.28460 72 27.610796   0.000
conditiontest   15.7008  55.55682  6  0.282608   0.787
 Correlation: 
              (Intr)
conditiontest -0.707

Standardized Within-Group Residuals:
       Min         Q1        Med         Q3        Max 
-2.6916143 -0.5418500  0.1988656  0.6273686  2.2428518 

Number of Observations: 80
Number of Groups: 8

Fixed or random effects

Fixed effects factors:

  • Informative factor levels with regard to the hypothesis
  • Effect of each level interesting
  • The levels are deliberately chosen by experimenter
  • Increasing sample size doesn’t increase number of levels

Random effects factors:

  • Uninformative factor levels with regard to the hypothesis
  • Effect of each level uninteresting
  • Increasing sample size often increases number of levels
  • Part of a population of possible levels

“one modeler’s random effect is another modeler’s fixed effect.”

“Are there enough levels of the factor in the data on which to base an estimate of the variance of the population of effects? No, means fixed effects.”

Fixed or random effects?

  • snake id number
  • vaccinated or not
  • species
  • light level
  • litter of puppies
  • site

Outer and inner variables

  • which design is more powerful?
  • which design is practical
mod3 <- lmer(Mass_g ~ condition + (1|tank), data = demo3)
summary(mod3)
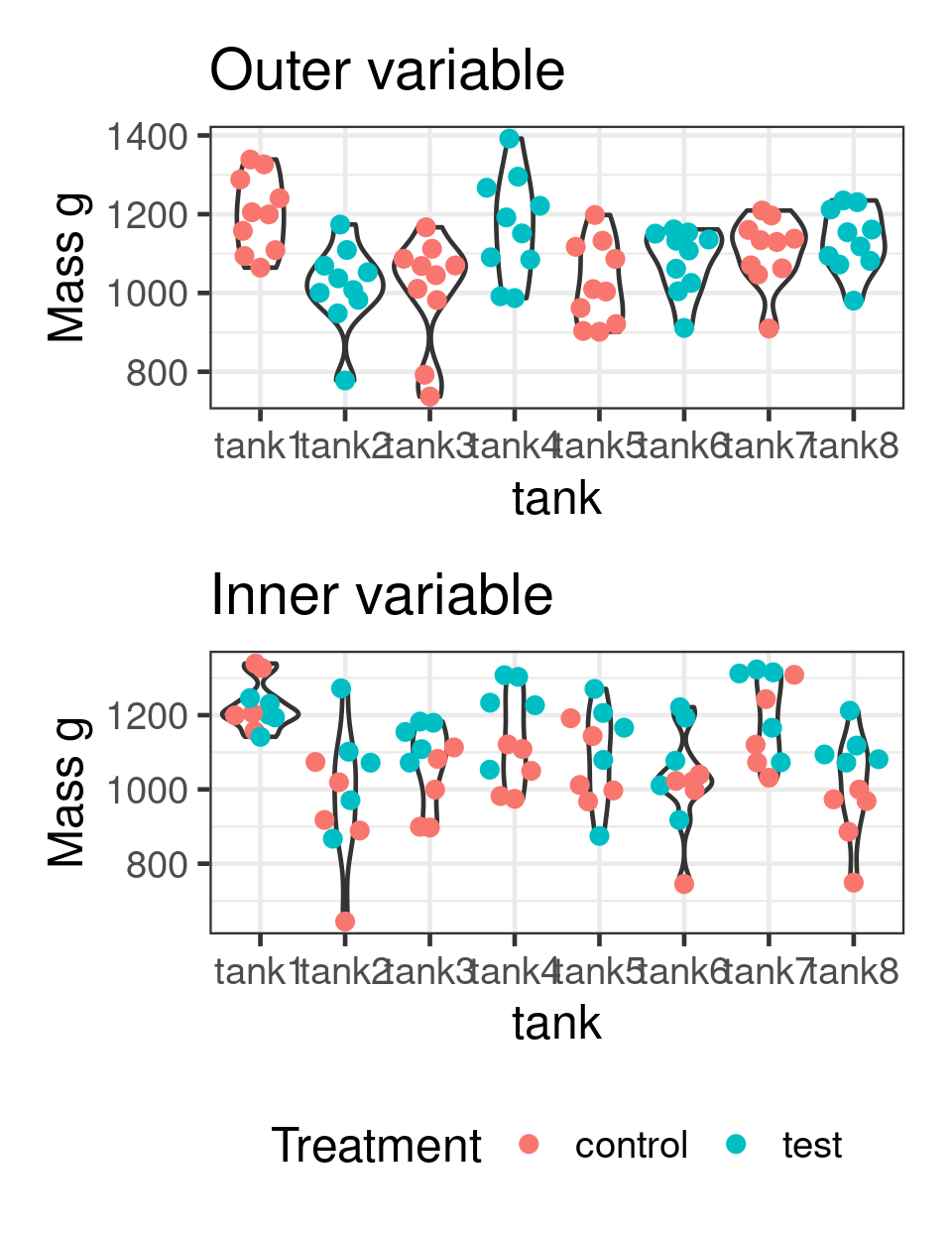
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Mass_g ~ condition + (1 | tank)
   Data: demo3

REML criterion at convergence: 975.8

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.72095 -0.58452  0.09483  0.55007  1.95600 

Random effects:
 Groups   Name        Variance Std.Dev.
 tank     (Intercept)  6371     79.82  
 Residual             12253    110.69  
Number of obs: 80, groups:  tank, 8

Fixed effects:
              Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)   1037.398     33.207    9.416  31.240 7.87e-11 ***
conditiontest  110.263     24.752   71.000   4.455 3.06e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr)
conditintst -0.373

Continuous inner predictor

data("sleepstudy", package = "lme4")

Random intercept

fm1 <- lmer(Reaction ~ Days + (1|Subject), sleepstudy, subset = Days>=2)

summary(fm1)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Reaction ~ Days + (1 | Subject)
   Data: sleepstudy
 Subset: Days >= 2

REML criterion at convergence: 1430

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.6261 -0.4450  0.0474  0.5199  4.1378 

Random effects:
 Groups   Name        Variance Std.Dev.
 Subject  (Intercept) 1746.9   41.80   
 Residual              913.1   30.22   
Number of obs: 144, groups:  Subject, 18

Fixed effects:
            Estimate Std. Error      df t value Pr(>|t|)    
(Intercept)  245.097     11.829  30.617   20.72   <2e-16 ***
Days          11.435      1.099 125.000   10.40   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
     (Intr)
Days -0.511
library(broom.mixed)
augment(fm1) |> 
  ggplot(aes(x = Days, y = Reaction, colour = Subject)) +
  geom_point() +
  geom_line(aes(y = .fitted)) +
  geom_line(aes(y = .fixed), colour = "black", size = 1.5) +
  theme(legend.position = "none")

Random slope

fm2 <- lmer(Reaction ~ Days + (Days|Subject), sleepstudy, subset = Days>=2)

summary(fm2)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Reaction ~ Days + (Days | Subject)
   Data: sleepstudy
 Subset: Days >= 2

REML criterion at convergence: 1404.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.0157 -0.3541  0.0069  0.4681  5.0732 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 Subject  (Intercept) 992.69   31.507        
          Days         45.77    6.766   -0.25
 Residual             651.59   25.526        
Number of obs: 144, groups:  Subject, 18

Fixed effects:
            Estimate Std. Error      df t value Pr(>|t|)    
(Intercept)  245.097      9.260  16.999  26.468 2.95e-15 ***
Days          11.435      1.845  17.001   6.197 9.74e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
     (Intr)
Days -0.454

Comparing models

anova(fm1, fm2)
Data: sleepstudy
Subset: Days >= 2
Models:
fm1: Reaction ~ Days + (1 | Subject)
fm2: Reaction ~ Days + (Days | Subject)
    npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
fm1    4 1446.5 1458.4 -719.25   1438.5                         
fm2    6 1425.2 1443.0 -706.58   1413.2 25.332  2  3.156e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model diagnostics

See ?plot.merMod

fm1F <- augment(fm1)
## standardized residuals versus fitted values
ggplot(fm1F, aes(x = .fitted, y = .resid)) + 
  geom_point(colour = "blue") +
  geom_hline(yintercept = 0)
## box-plots of residuals by Subject
ggplot(fm1F, aes(x = Subject, y = .resid)) + 
  geom_boxplot() + 
  coord_flip()
ggplot(fm1F, aes(x = .fitted, y = Reaction)) + 
  geom_point(colour = "blue") +
    facet_wrap(facets = vars(Subject)) +
  geom_abline(intercept = 0, slope = 1)
#qq plot of residuals
library(lattice)
qqmath(fm1)
#qq plot of random effects
qqmath(ranef(fm1))
$Subject

performance package

performance::check_model(fm1)

Crossed random effects

Two random effects

Eggs from birds nests (first random effect - lay_nest) moved to other nests (second random effect - hatch_nest)

lmer(mass ~ treatment + (1|lay_nest) + (1|hatch_nest), data = data)

Nested random effects

Hierarchical random effects

  • Plot nested in site
  • sample nested in fish nested in tank
  • species nested in family
lmer(mass ~ treatment + (1|site/plot), data = data)

Convergence & other problems

Sometimes mixed effect models report errors.

Take them seriously.

May need to simplify the model

Having predictors on same scale can help

Beyond linear mixed effect models

Generalised linear mixed effect models

  • poisson
  • binomial

Fit with glmer()

Autocorrelated data

  • repeat measurements
  • fit with nlme::lme()

Bayesian hierarchial models

Mixed effect models can be hard to fit

  • convergence problems

Bayesian model can help

Different statistical philosophy

  • rstan
  • nimble

Use prior information (or uninformative priors)

Resources

Bolker B (2021) GLMM FAQ

Harrison et al (2018) A brief introduction to mixed effects modelling and multi-model inference in ecology