Descriptive statistics and Introduction to statistical inference

Bio300B Lecture 6

Richard J. Telford (Richard.Telford@uib.no)

Institutt for biovitenskap, UiB

25 September 2024

Describing a distribution

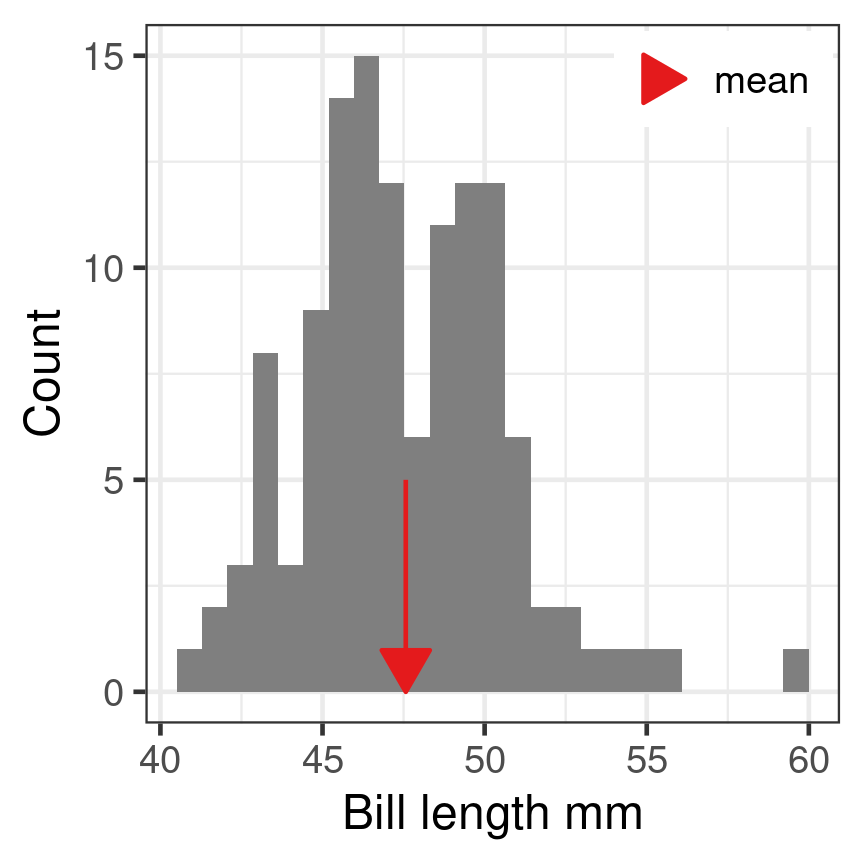
Midpoint

Mean

\[\overline{x} = \frac{\sum_{i=1}^n x_i}{n}\]

  • Sum of all observations divided by number of observations
  • Centre of gravity of the data
  • mean()

Median

  • Sort from minimum to maximum
  • Observation in the middle is the median
  • median()

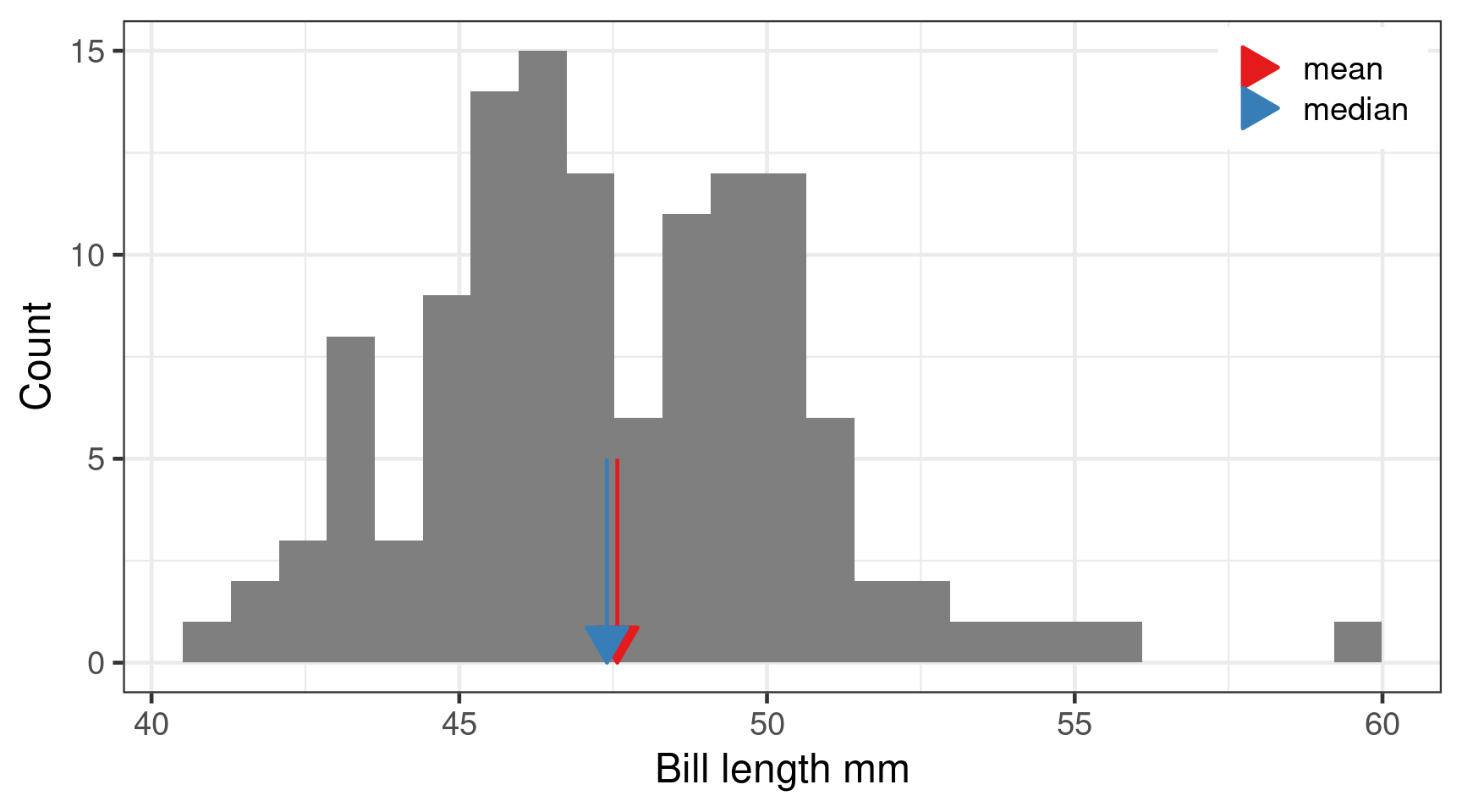
Mean vs Median

Mean vs Median

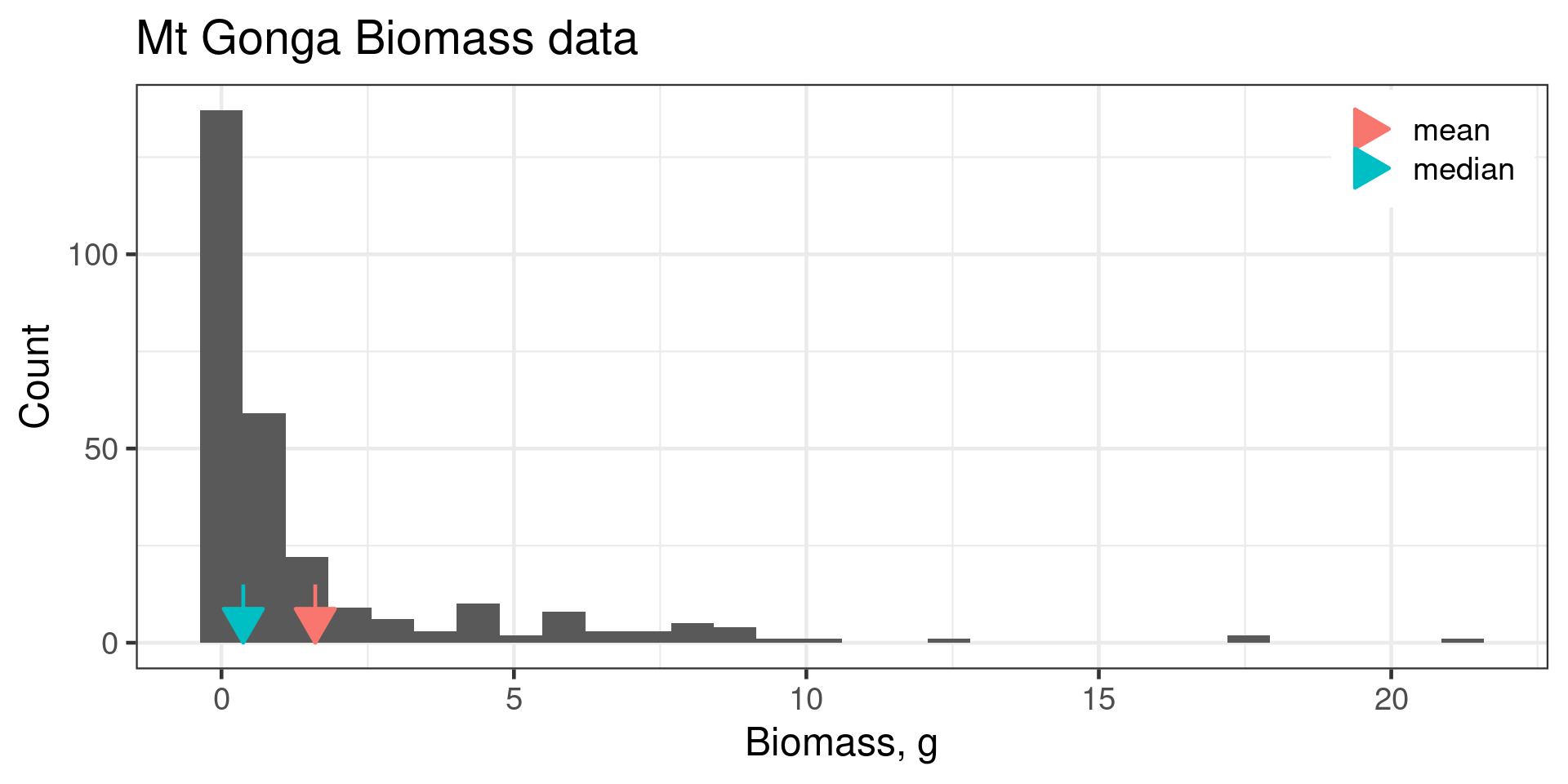
Calculating Mean and Median in R

vec <- c(56.7, 57.2, 62.7, 56.4, 60.8)
# mean of a vector
mean(vec)
[1] 58.76
# median of a vector
median(vec)
[1] 57.2

Use na.rm = TRUE to remove missing values.

vec <- c(56.7, 57.2, 62.7, 56.4, 60.8, NA)
# mean of a vector with NA
mean(vec)
[1] NA
# mean of a vector excluding NA
mean(vec, na.rm = TRUE)
[1] 58.76
# median of a column
median(penguins$bill_length_mm, na.rm = TRUE)
[1] 44.45
# or
penguins |>
  summarise(med = median(bill_length_mm, na.rm = TRUE))
# A tibble: 1 × 1
    med
  <dbl>
1  44.4
# mean of a column with a grouping variable
penguins |>
  group_by(species) |>
  summarise(
    med = median(bill_length_mm, na.rm = TRUE),
    .groups = "drop"
  )
# A tibble: 3 × 2
  species     med
  <fct>     <dbl>
1 Adelie     38.8
2 Chinstrap  49.6
3 Gentoo     47.3

Spread

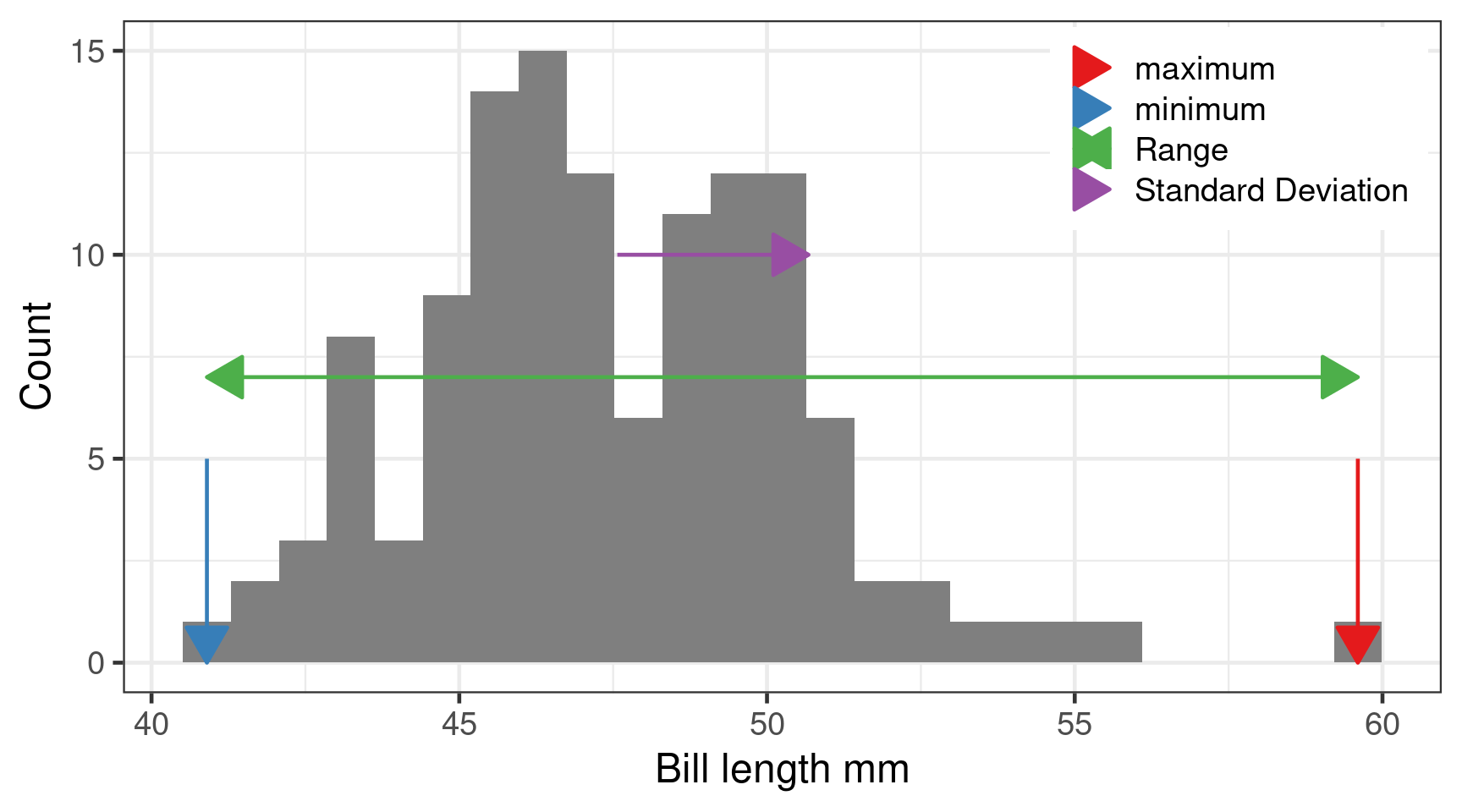
Minimum, maximum and range

  • min()
  • max()

Range is difference between smallest and largest.

# range() gives smallest and largest values
range(penguins$bill_length_mm, na.rm = TRUE)
[1] 32.1 59.6
# calculate range as
max(penguins$bill_length_mm, na.rm = TRUE) -
  min(penguins$bill_length_mm, na.rm = TRUE)
[1] 27.5
# or
diff(range(penguins$bill_length_mm, na.rm = TRUE))
[1] 27.5

Variance

The average squared distance around the mean var()

Population variance

\[\sigma^2 = \frac{\sum_{i=1}^n (x_i - \mu)^2}{n}\] Where \(\mu\) is the population mean.

Sample variance

\[s^2 = \frac{\sum_{i=1}^n (x_i - \overline{x})^2}{n-1}\] Where \(\overline{x}\) is the sample mean.

Standard deviation

Square root of the variance \[s = \sqrt{s^2}\] \[s = \sqrt{\frac{\sum_{i=1}^n (x_i - \overline{x})^2}{n-1}}\] Same units as variable

sqrt(var())
sd()

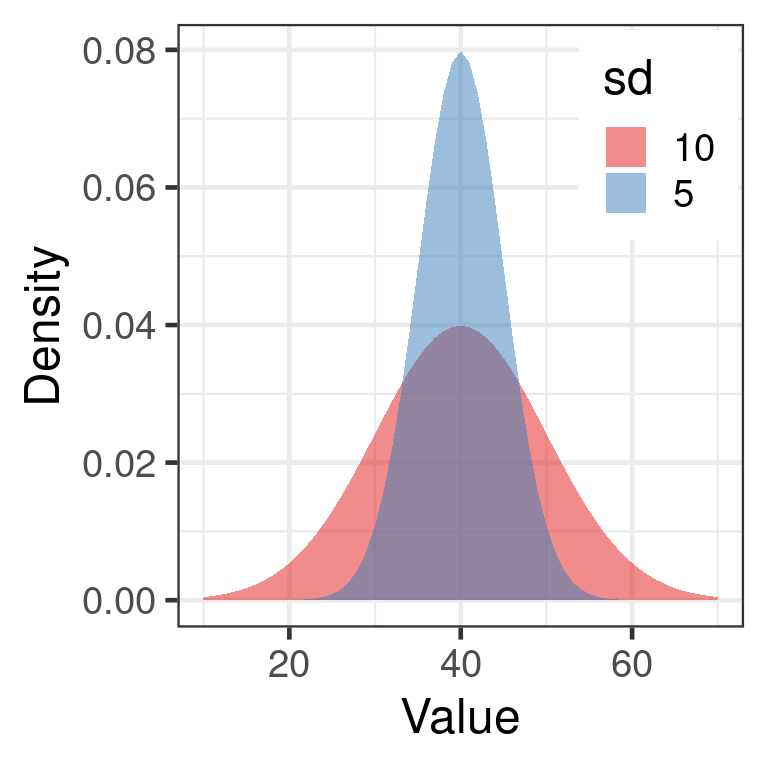
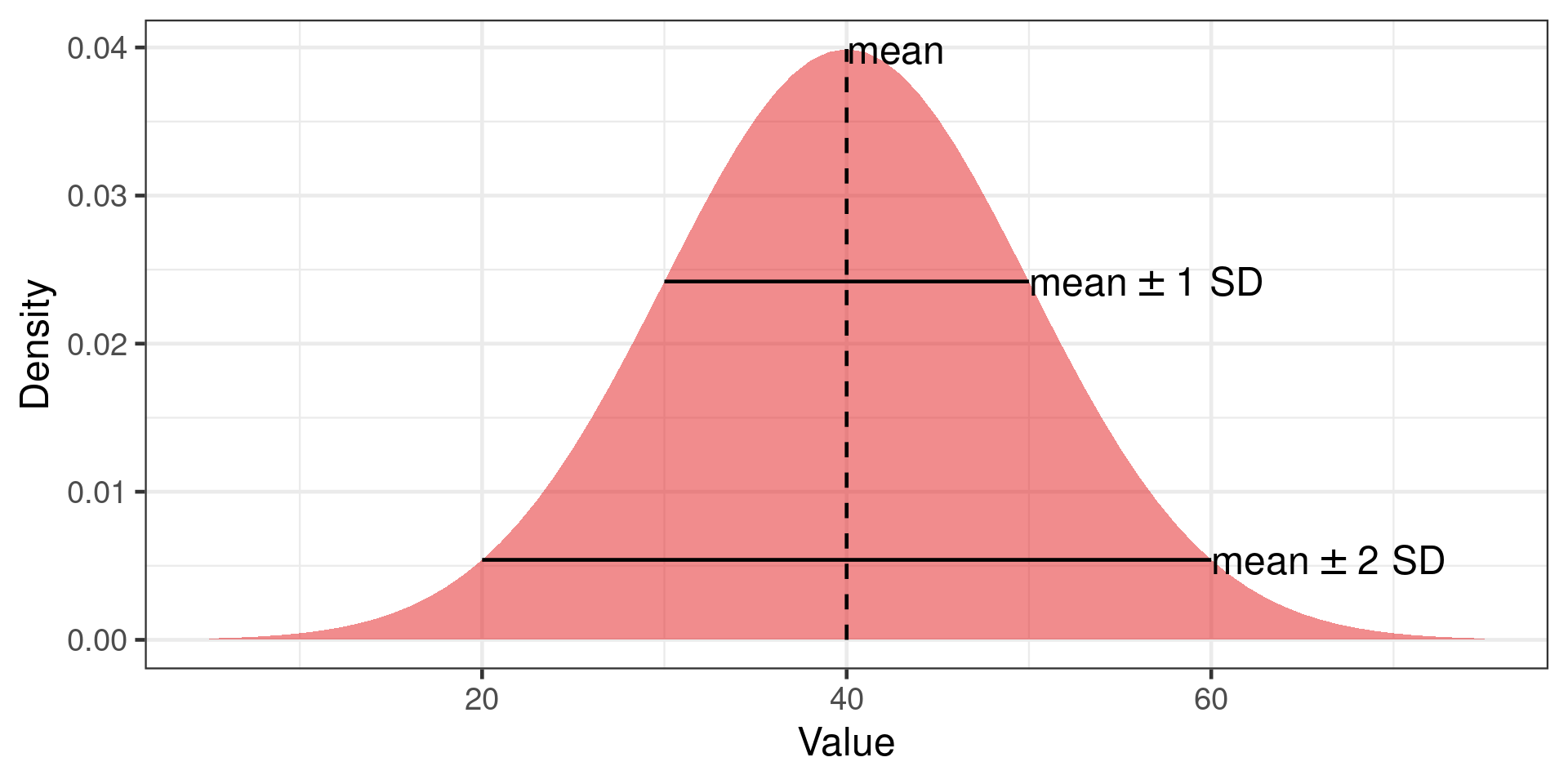
Higher moments

Skew

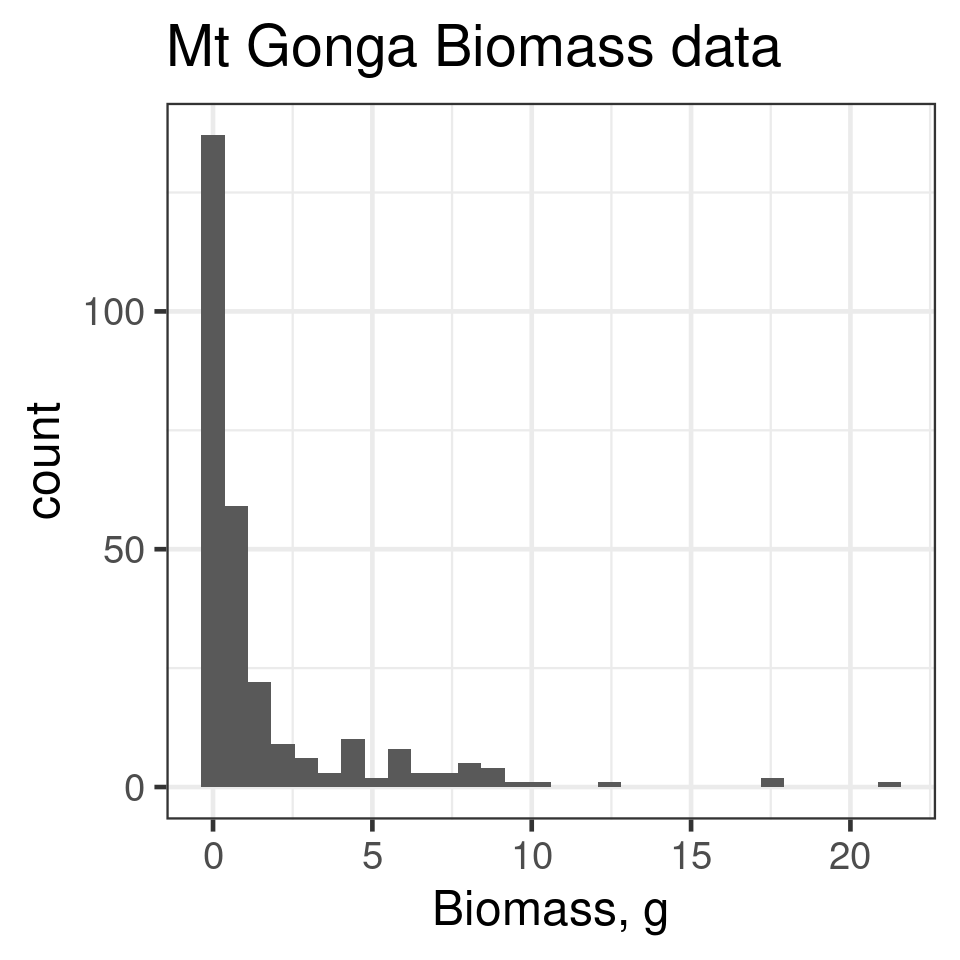
Right skew
positive skew e1071::skewness()

Kurtosis

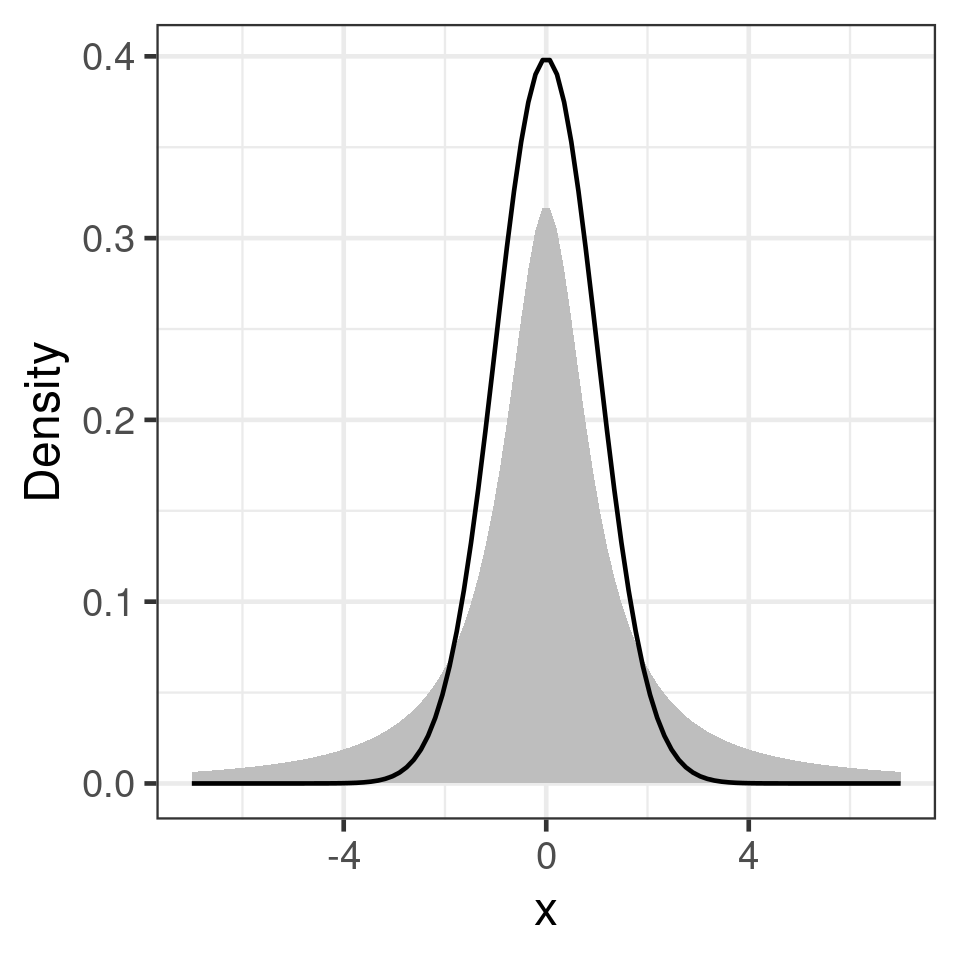
heavy tails

e1071::kurtosis()

Making inferences about the population

Sample: 123 Gentoo penguins

Population: All Gentoo penguins in the Palmer Archipelago.

What can we infer about the population from the sample?

Uncertainty in the mean

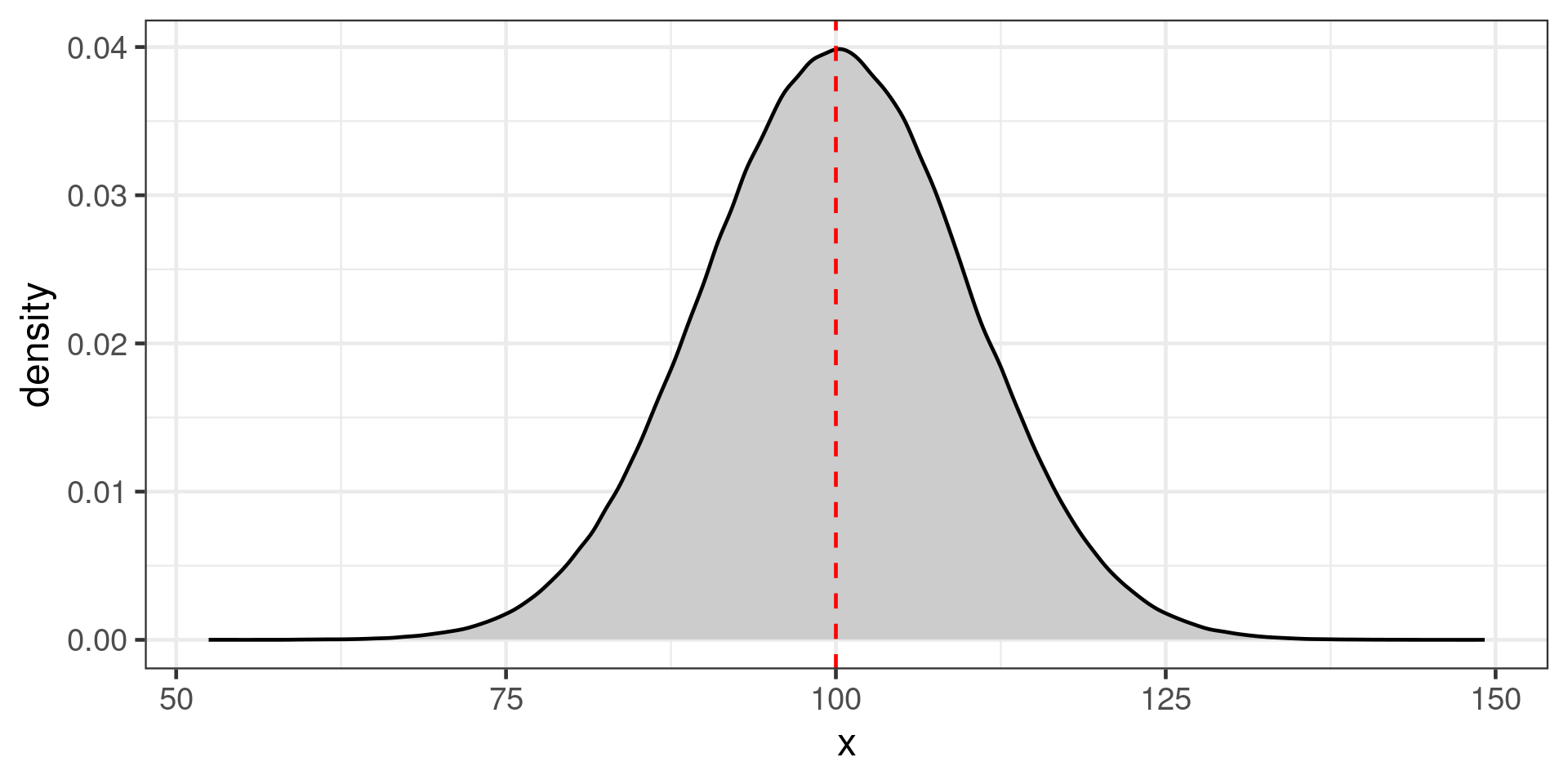
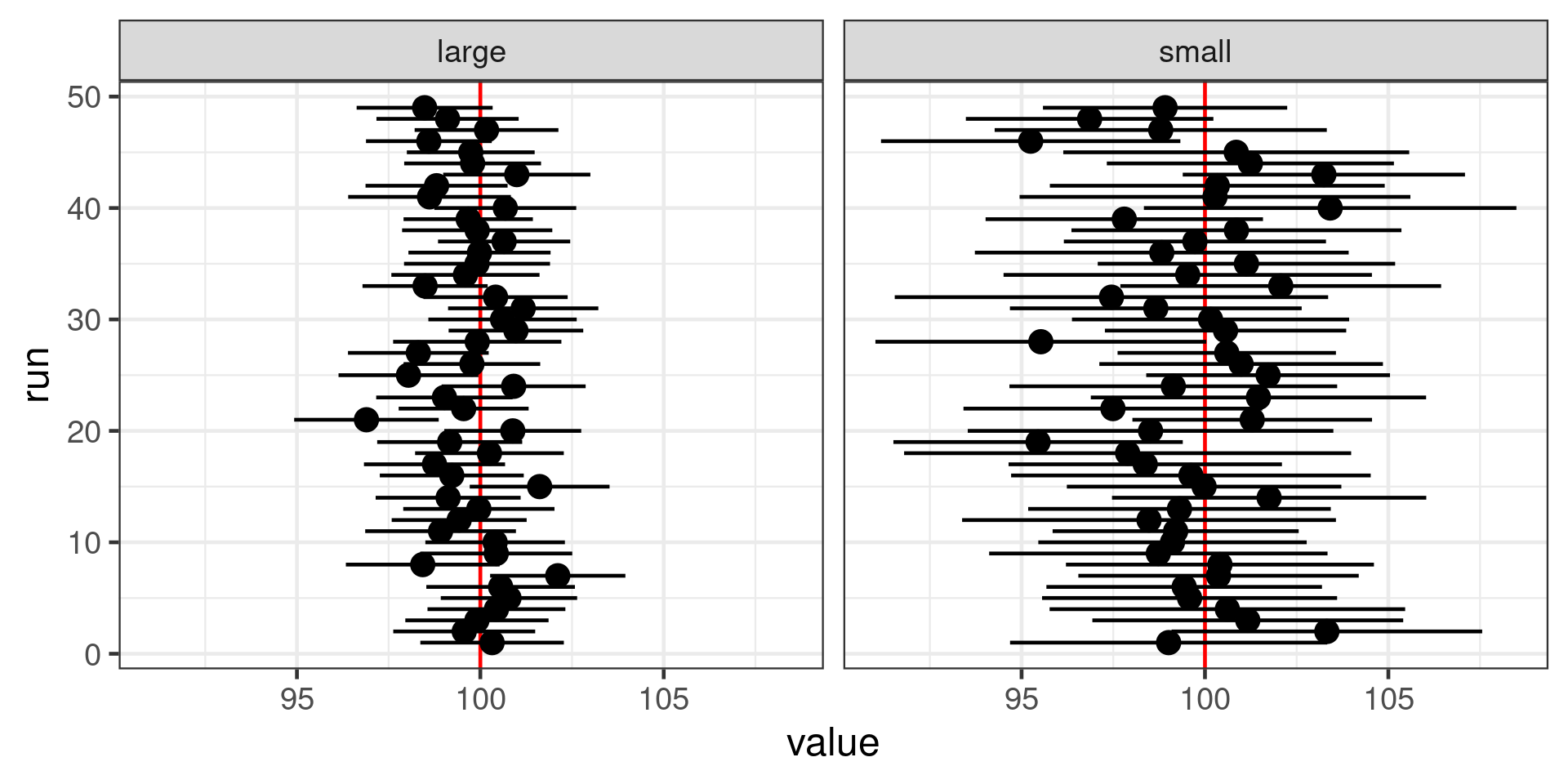
Population of 1,000,000 indviduals

Large (100 individuals) or small (20 individuals) samples

Histograms of samples

NULL

Histogram of sample means

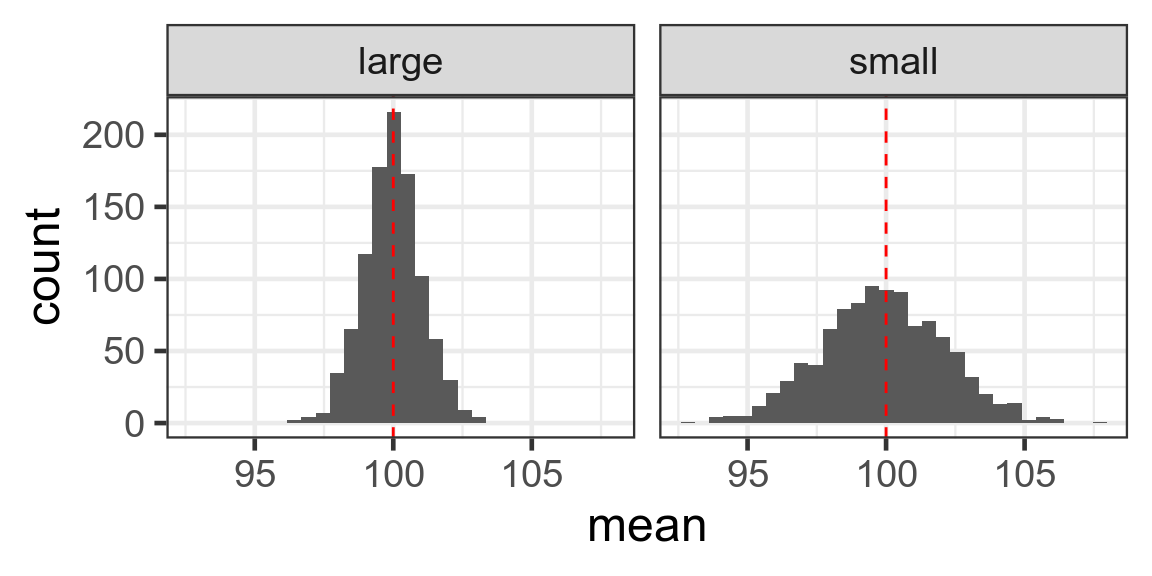
Standard error of the mean

Standard deviation divided by square root of number of observations

\[SE = \frac{s}{\sqrt{n}}\] Large n - small SE - reliable estimate of mean

Small n - large SE - less reliable estimate of mean

Confidence interval

If experiment repeated many times, confidence level represents the proportion of confidence intervals that contain the true value of the unknown population parameter.

95% confidence interval will contain true value in 95% of repeat experiments

Easily misunderstood.

(Bayesian credibility intervals are much more intuitive)

Confidence interval of the mean

95% confidence interval

Mean \(\pm\) 1.96 * SE

Why 1.96?

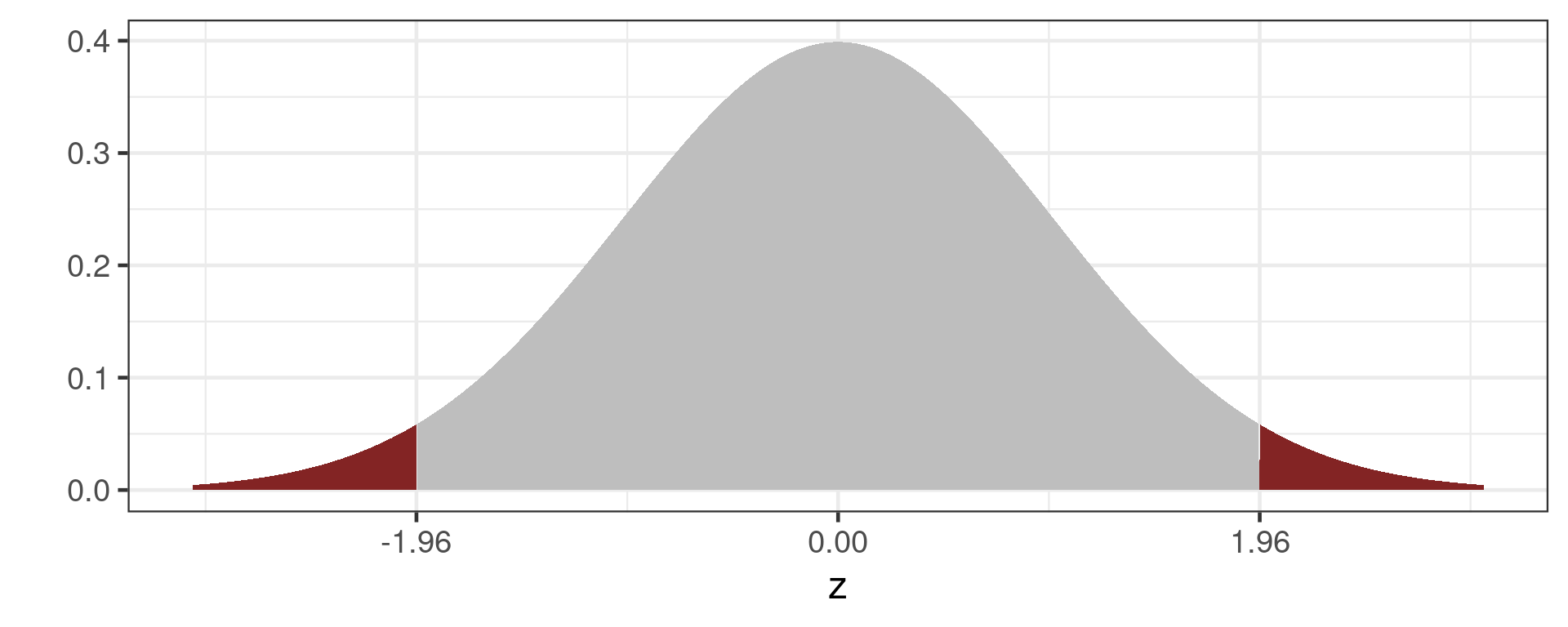
Grey area is 95% of the normal distribution

Estimated means with 95% confidence interval for different sample sizes

Choosing a statistical test

  1. What is the hypothesis?
  2. What is the underlying distribution of your response variable?
  3. What type of the predictor(s)?
  4. What type of observational or experimental design do you have?

The hypothesis

The statistical hypothesis needs to match your scientific hypothesis

Hypothesis example:
H0: The bill length of Gentoo penguins does not depend on sex.

The predictors

  • Categorical (sex, species)
  • Continuous (body mass)
  • both (with > 1 predictor)

Need to know so we can code predictor variables and interpret the output of our models.

The response

  • Continuous (bill length)
  • count (number of penguins)
  • binary (sex, survived/died)
  • proportion (8 out of 10)

Statistical model families (lm, lme, glm etc.) differ in assumptions about the underlying distribution of the response variable.

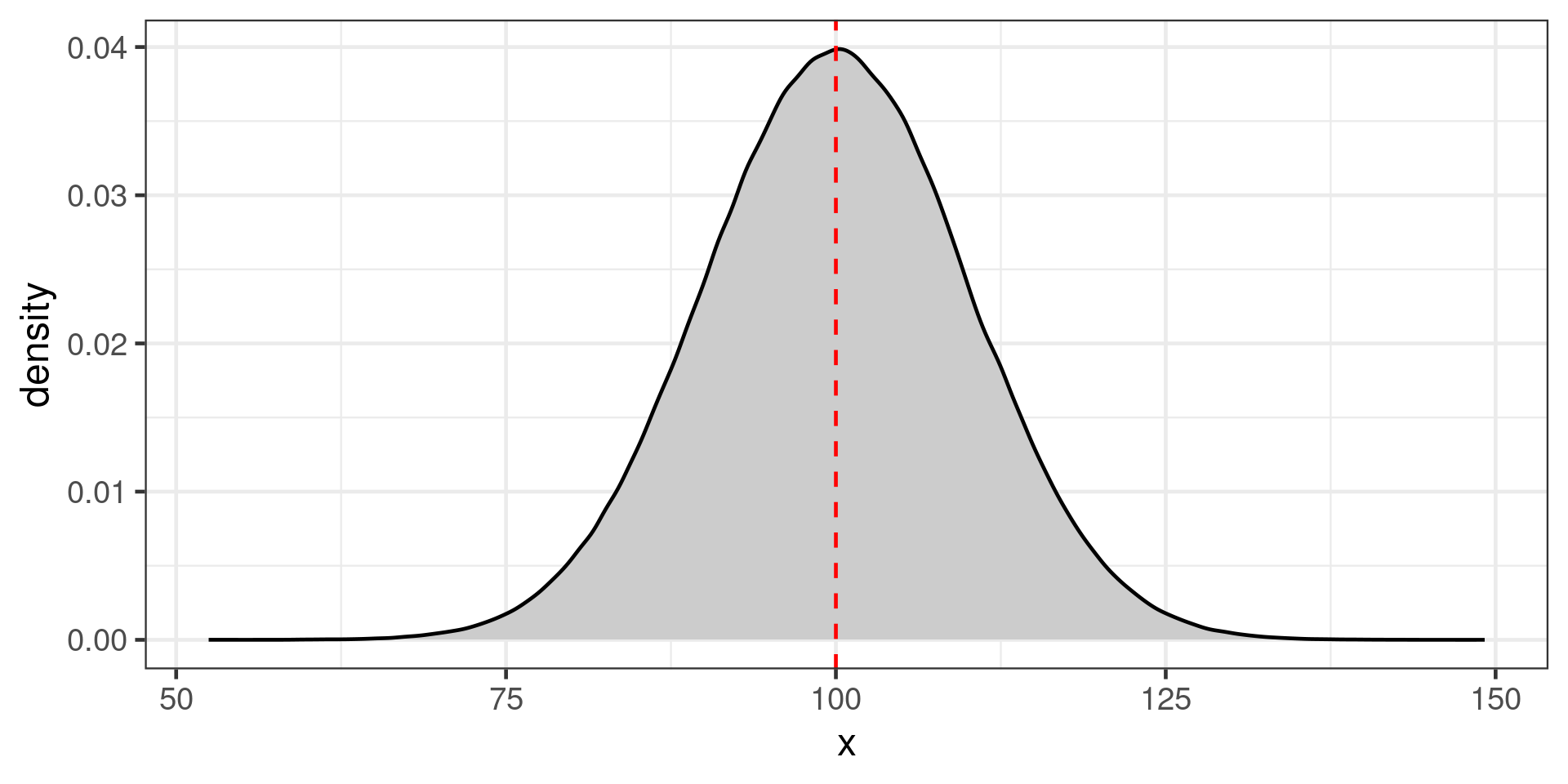
Gaussian (Normal) distribution

Often assumed for continuous distributions, body mass, egg shell thickness

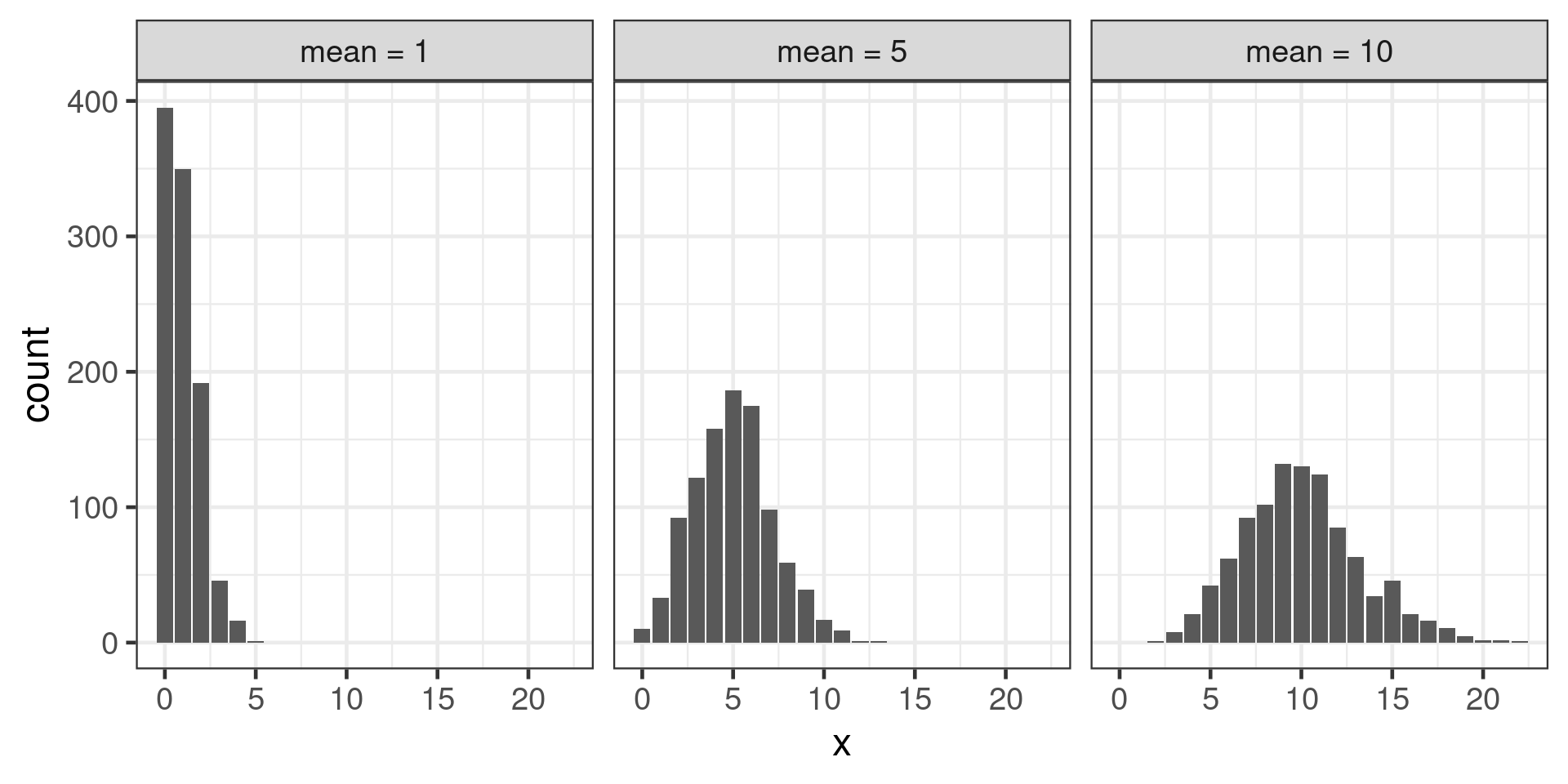
Poisson distribution

Count data

Shape varies with mean

Experimental design

  • Independent observations?
  • time series?
  • clustered design?

Key

  • Independent observations
    • Continuous response = linear models (lm(), t.test())
    • Count/binary/proportion = generalised linear models (glm())
  • Clustered observations
    • Continuous response = linear mixed effect models (lme(), lmer())
    • Count/binary/proportion = generalised linear mixed effect models (glmer())

A t-test

Compare means

H0: Bill length does not depend on sex in Gentoo penguins

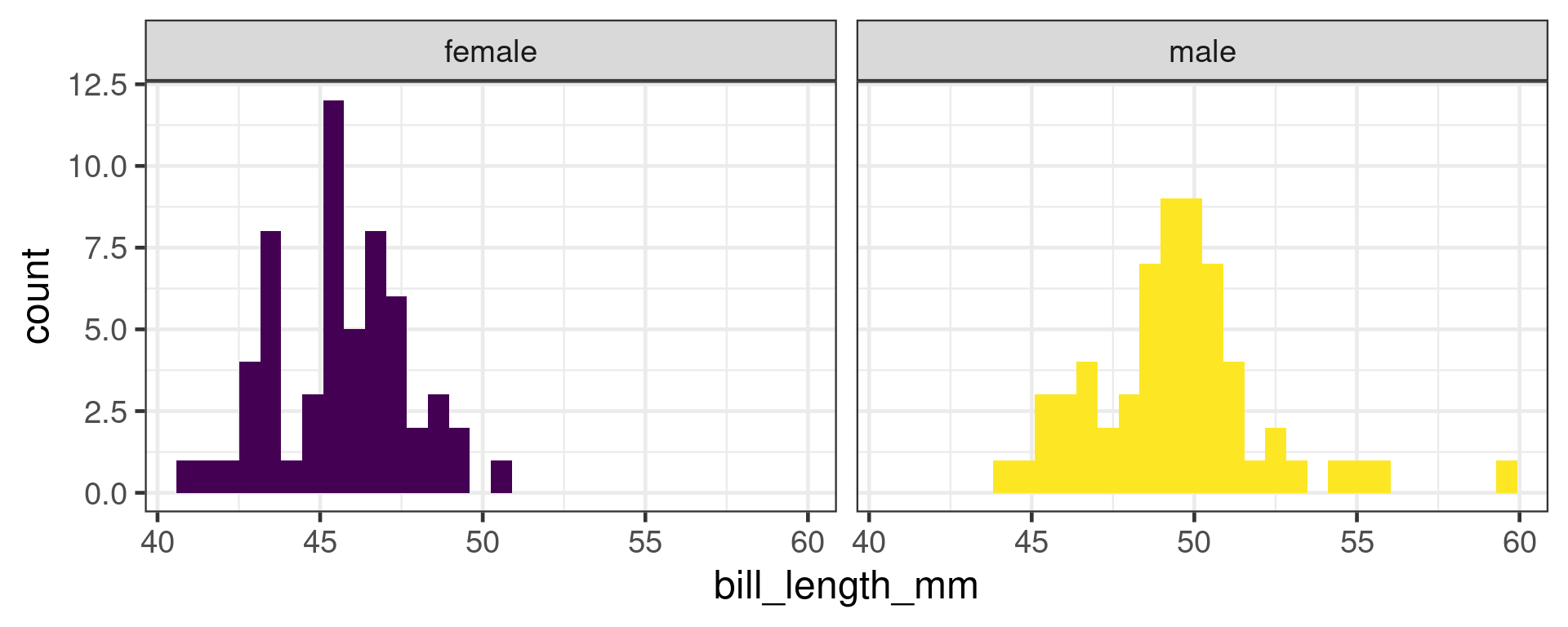
t-test in R

gentoo <- penguins |>
  filter(species == "Gentoo") |>
  drop_na(bill_length_mm, sex)

mod1 <- t.test(bill_length_mm ~ sex, data = gentoo)

    Welch Two Sample t-test

data:  bill_length_mm by sex
t = -8.8798, df = 111.31, p-value = 1.315e-14
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
 -4.782478 -3.037477
sample estimates:
mean in group female   mean in group male 
            45.56379             49.47377

P values

Often misinterpreted

  • Not a measure of effect size or practical significance
  • Not the probability that hypothesis is true
  • Strongly affected by sample size

If there were actually no effect (if the true difference between means were zero) then the probability of observing a value for the difference equal to, or greater than, that actually observed would be p=0.05.

Many assumptions

Confidence intervals are more interpretable

Type 1 and type 2 errors

Null hypothesis is True False

Rejected

Type I error
False positive

Correct decision
True positive

Not rejected

Correct decision
True negative

Type II error
False negative

One sided Z-test

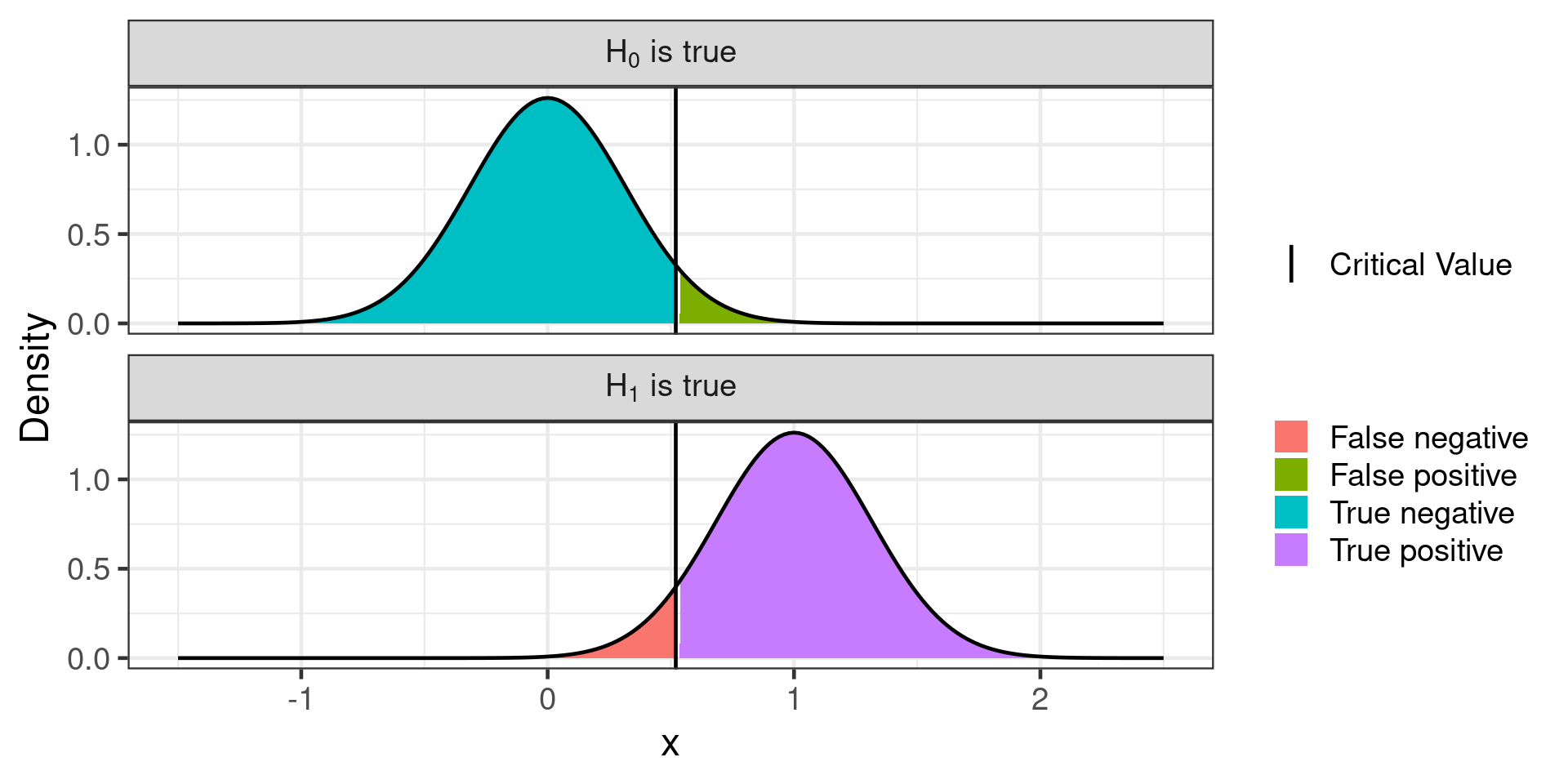
#| label: power-app
#| standalone: true
#| viewerHeight: 600

library(shiny)

ui <-  fluidPage(
        # Application title
      titlePanel("One sided Z-test"),
      sidebarLayout(
          sidebarPanel(
            sliderInput("delta", "True mean", value = 1, min = 0.1, max = 2),
            sliderInput("sd", "Standard deviation", value = 1, min = 0.5, max = 2),
            sliderInput("n", "Sample size, n", value = 10, min = 10, max = 100),
            radioButtons("alpha", "Significance level, alpha", choices = c(0.05, 0.01, 0.001), selected = 0.05)
         ),
            # Show a plot of the generated distribution
          mainPanel(
             plotOutput("distPlot")
          )
))

server <- function(input, output, session) {
  output$distPlot <- renderPlot({
    n <- input$n
    alpha <- as.numeric(input$alpha)
    delta <- input$delta
    sd <- input$sd
    mx <- 2.5
    mn <- -1.5
    crit <-
      qnorm(
        alpha,
        mean = 0,
        sd = sd / sqrt(n),
        lower.tail = FALSE
      )
    H0 <- data.frame(x = seq(mn, mx, length = 201))
    H0$y <- dnorm(x = H0$x, mean = 0, sd = sd / sqrt(n))
    H0$what <- ifelse(H0$x < crit, yes = "True negative", no = "False positive")
    H0$hypothesis <- "H[0]"

    H1 <- data.frame(x = seq(mn, mx, length = 201))
    H1$y <- dnorm(x = H1$x, mean = delta, sd = sd / sqrt(n))
    H1$what <- ifelse(H1$x < crit, yes = "True negative", no = "False positive")
    H1$hypothesis <- "H[1]"

    par(oma=c(2,2,0,0), mar=c(1.2,2,2,1), mfrow=c(2,1), cex = 1.5, tcl = -0.1, mgp = c(3, 0.2, 0))
    plot(H0$x, H0$y, type = "n", main = expression(H[0]~is~true), xlab = "", ylab = "")
    polygon(H0$x, H0$y)
    polygon(c(H0$x[H0$x > crit][1], H0$x[H0$x > crit]), c(0, H0$y[H0$x > crit]), col = "#832424")
    abline(v = crit)
   
    plot(H1$x, H1$y, type = "n", main = expression(H[1]~is~true), xlab = "", ylab = "")
    polygon(H1$x, H1$y)
    polygon(c(H1$x[H1$x > crit][1], H1$x[H1$x > crit]), c(0, H1$y[H1$x > crit]), col = "#832424")
    abline(v = crit) 
    mtext(text="x",side=1,line=0,outer=TRUE, 1.5)
    mtext(text="Density",side=2,line=0,outer=TRUE, cex = 1.5)
    
  })
}

shinyApp(ui, server)

The need for power

With little power:

  • May not be able to reject H0 when it is false
  • Exaggerate effect size

Lots of power

  • Probably can reject H0 when it is false
  • More precise estimates of effect size
  • More expensive

Need to do power analysis before experiment.

Components of a power analysis

  • Effect size
  • Type I error rate (significance level - conventionally set to 0.05)
  • Power (1 - Type II error rate) - conventionally aim for 0.8
  • Number of observations

Can solve for any of these

Typically want to know how many observations needed.

Analytic power analysis

Some power tests in base R.

  • power.t.test
  • power.anova.test
  • power.prop.test

More in pwr package

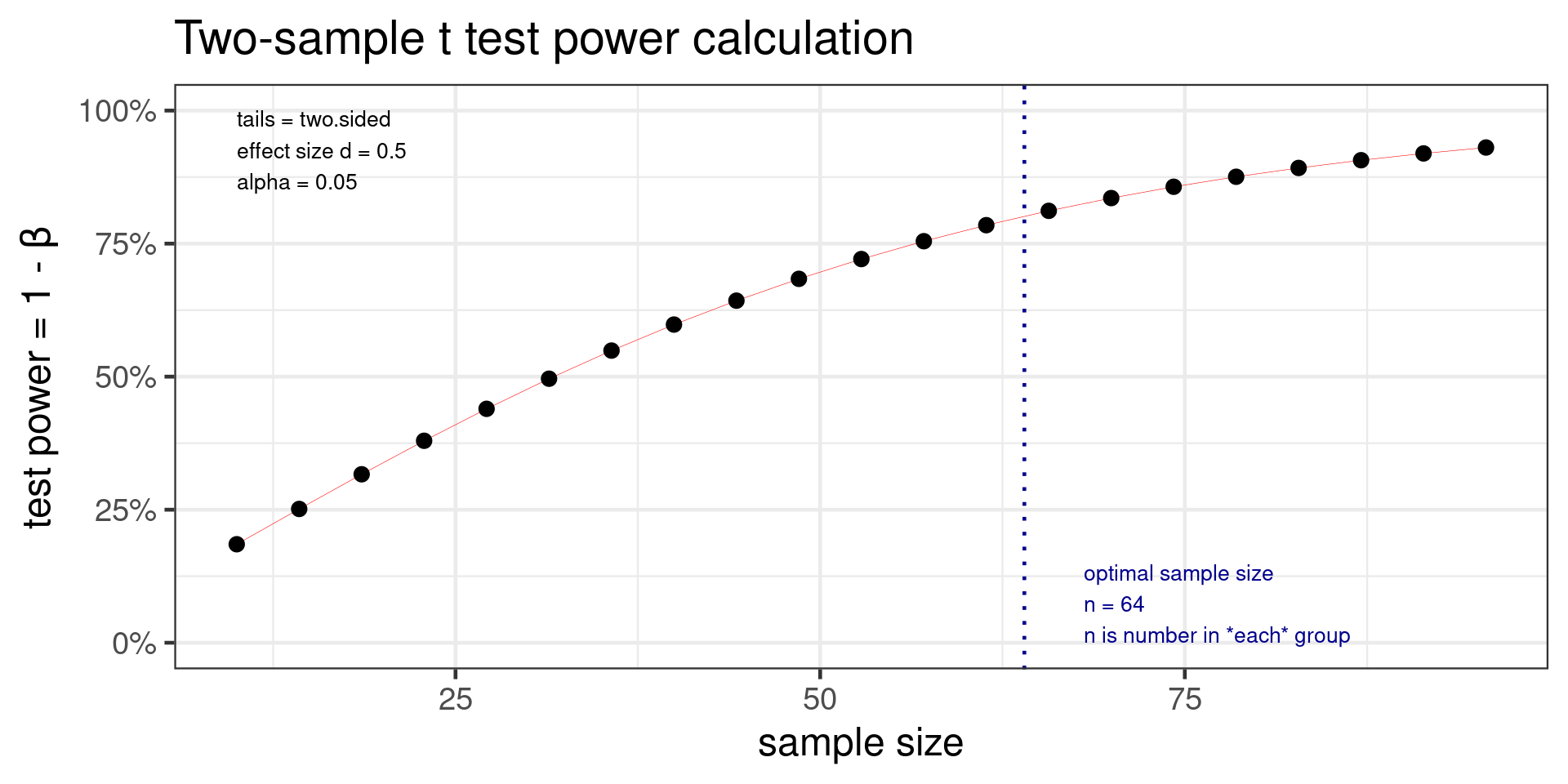
Power t test

library("pwr")
pow <- pwr.t.test(d = 0.5, sig.level = 0.05, power = 0.8)
pow

     Two-sample t test power calculation 

              n = 63.76561
              d = 0.5
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

Effect size is Cohen’s d \(d = \frac{\mu_1 - \mu_2}{\sigma}\)

  • Power test should be done before experimental work to determine sample size
  • Analytical and simulation approaches are possible
  • Key challenge is estimating effect size
    • existing estimates are likely biased
    • minimum interesting effect size