Multiple Regression

Bio300B Lecture 8

Richard J. Telford (Richard.Telford@uib.no)

Institutt for biovitenskap, UiB

11 October 2025

Outline

  • Types of models
  • Interactions
  • Model selection
    • Exploratory data analysis
    • Anova for hypothesis testing
  • Multi-collinearity
  • Autocorrelation
  • Reporting statistics

Adding more variables

# Two way anova - two categorical predictors
mod_anova2 <- lm(bill_length_mm ~ sex + species, data = penguins)

# ancova - one categorical one continuous predictor
mod_ancova <- lm(bill_length_mm ~ sex + flipper_length_mm, data = penguins)

# Multiple regression - two continuous
mod_mult <- lm(bill_length_mm ~ body_mass_g + flipper_length_mm, data = penguins)
summary(mod_anova2)

Call:
lm(formula = bill_length_mm ~ sex + species, data = penguins)

Residuals:
   Min     1Q Median     3Q    Max 
-6.087 -1.377 -0.071  1.225 11.013 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)        36.977      0.231   160.2   <2e-16 ***
sexmale             3.694      0.255    14.5   <2e-16 ***
speciesChinstrap   10.010      0.341    29.3   <2e-16 ***
speciesGentoo       8.698      0.287    30.3   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.32 on 329 degrees of freedom
  (11 observations deleted due to missingness)
Multiple R-squared:  0.821, Adjusted R-squared:  0.819 
F-statistic:  503 on 3 and 329 DF,  p-value: <2e-16
summary(mod_ancova)

Call:
lm(formula = bill_length_mm ~ sex + flipper_length_mm, data = penguins)

Residuals:
   Min     1Q Median     3Q    Max 
-9.720 -2.812 -0.812  2.021 19.764 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        -4.4669     3.2364   -1.38     0.17    
sexmale             2.0727     0.4568    4.54    8e-06 ***
flipper_length_mm   0.2359     0.0163   14.46   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.03 on 330 degrees of freedom
  (11 observations deleted due to missingness)
Multiple R-squared:  0.46,  Adjusted R-squared:  0.457 
F-statistic:  141 on 2 and 330 DF,  p-value: <2e-16
summary(mod_mult)

Call:
lm(formula = bill_length_mm ~ body_mass_g + flipper_length_mm, 
    data = penguins)

Residuals:
   Min     1Q Median     3Q    Max 
-8.806 -2.590 -0.705  1.991 18.829 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -3.436694   4.580553   -0.75     0.45    
body_mass_g        0.000662   0.000567    1.17     0.24    
flipper_length_mm  0.221865   0.032348    6.86  3.3e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.12 on 339 degrees of freedom
  (2 observations deleted due to missingness)
Multiple R-squared:  0.433, Adjusted R-squared:  0.43 
F-statistic:  129 on 2 and 339 DF,  p-value: <2e-16

Different formula

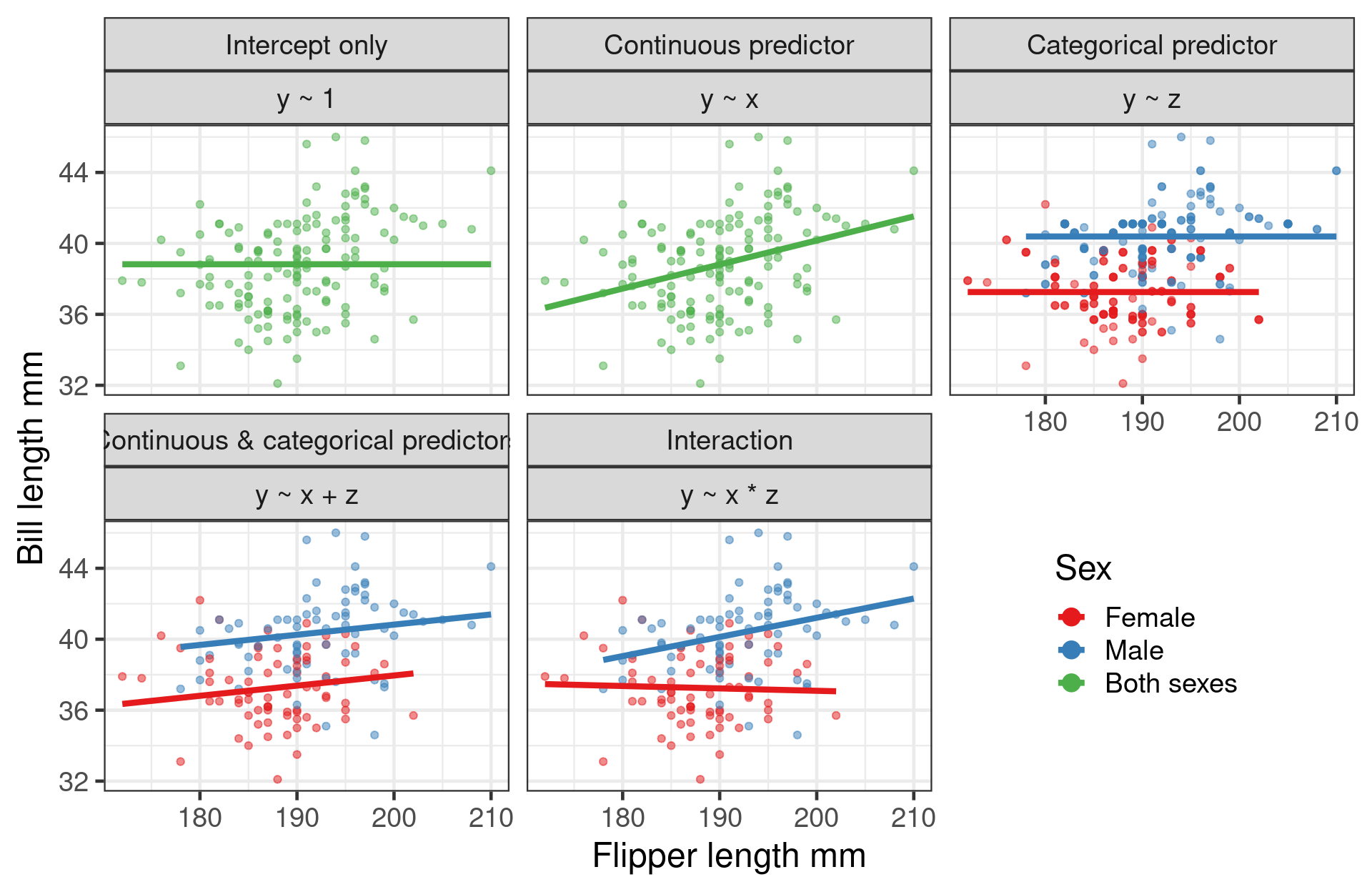
What is an interaction

Effect of one predictor depends on value of another

Interaction between categorical predictors

mod <- lm(flipper_length_mm ~ species * sex, data = penguins)
summary(mod)

Call:
lm(formula = flipper_length_mm ~ species * sex, data = penguins)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.795  -3.411   0.088   3.459  17.589 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept)               187.795      0.662  283.72  < 2e-16 ***
speciesChinstrap            3.941      1.174    3.36  0.00088 ***
speciesGentoo              24.912      0.995   25.04  < 2e-16 ***
sexmale                     4.616      0.936    4.93  1.3e-06 ***
speciesChinstrap:sexmale    3.560      1.661    2.14  0.03278 *  
speciesGentoo:sexmale       4.218      1.397    3.02  0.00274 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.66 on 327 degrees of freedom
  (11 observations deleted due to missingness)
Multiple R-squared:  0.84,  Adjusted R-squared:  0.837 
F-statistic:  342 on 5 and 327 DF,  p-value: <2e-16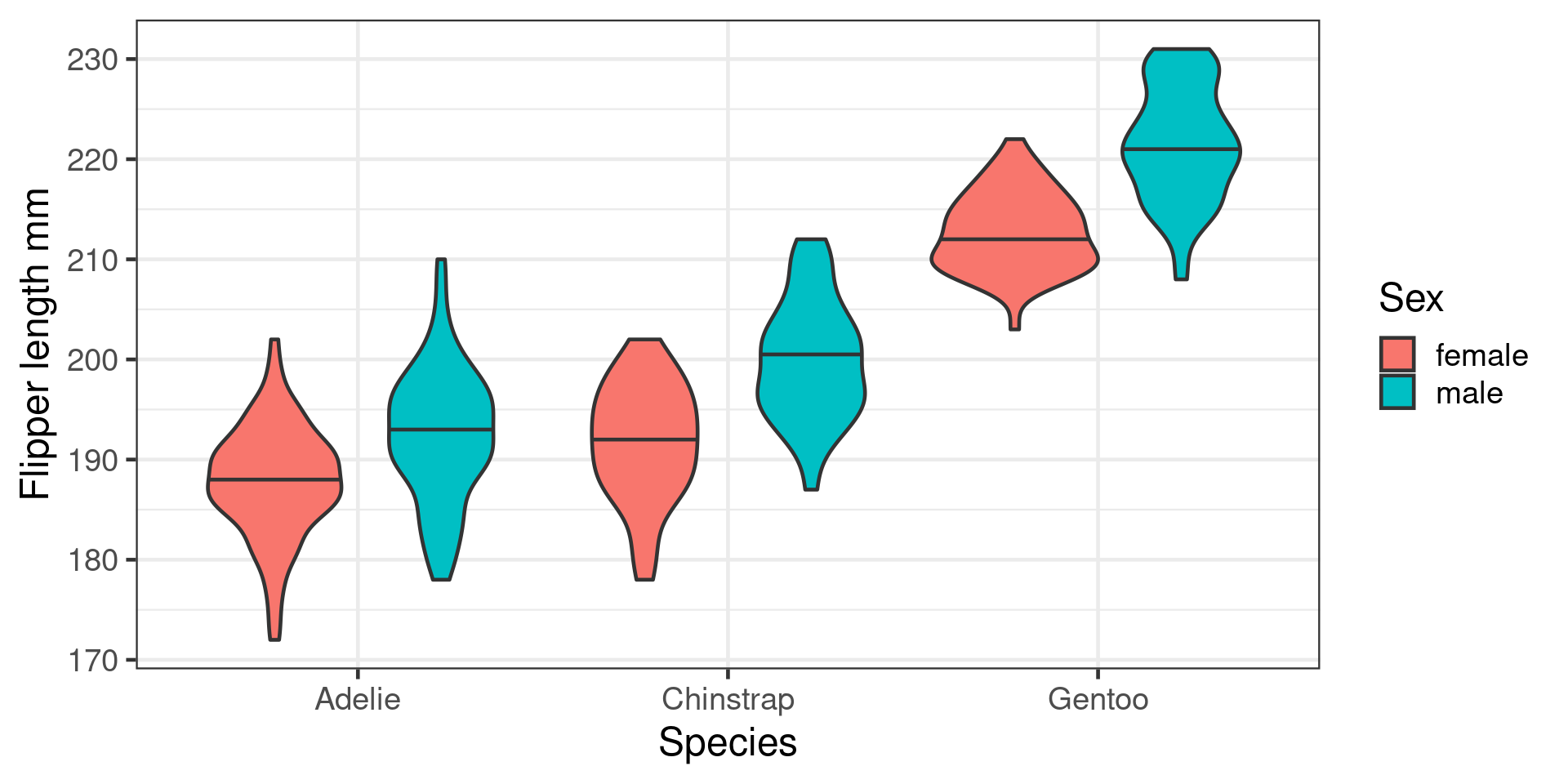

Understanding coefficients

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| label: coef-explain
#| standalone: true
#| viewerHeight: 700
#| echo: false


library(shiny)
library(bslib)

penguins <- structure(list(species = structure(c(1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 2L, 2L, 
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
2L, 2L), levels = c("Adelie", "Chinstrap", "Gentoo"), class = "factor"), 
    island = structure(c(3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
    3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 3L, 
    3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 
    3L, 3L, 3L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
    1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
    2L, 2L, 2L, 2L, 2L), levels = c("Biscoe", "Dream", "Torgersen"
    ), class = "factor"), bill_len = c(39.1, 39.5, 40.3, NA, 
    36.7, 39.3, 38.9, 39.2, 34.1, 42, 37.8, 37.8, 41.1, 38.6, 
    34.6, 36.6, 38.7, 42.5, 34.4, 46, 37.8, 37.7, 35.9, 38.2, 
    38.8, 35.3, 40.6, 40.5, 37.9, 40.5, 39.5, 37.2, 39.5, 40.9, 
    36.4, 39.2, 38.8, 42.2, 37.6, 39.8, 36.5, 40.8, 36, 44.1, 
    37, 39.6, 41.1, 37.5, 36, 42.3, 39.6, 40.1, 35, 42, 34.5, 
    41.4, 39, 40.6, 36.5, 37.6, 35.7, 41.3, 37.6, 41.1, 36.4, 
    41.6, 35.5, 41.1, 35.9, 41.8, 33.5, 39.7, 39.6, 45.8, 35.5, 
    42.8, 40.9, 37.2, 36.2, 42.1, 34.6, 42.9, 36.7, 35.1, 37.3, 
    41.3, 36.3, 36.9, 38.3, 38.9, 35.7, 41.1, 34, 39.6, 36.2, 
    40.8, 38.1, 40.3, 33.1, 43.2, 35, 41, 37.7, 37.8, 37.9, 39.7, 
    38.6, 38.2, 38.1, 43.2, 38.1, 45.6, 39.7, 42.2, 39.6, 42.7, 
    38.6, 37.3, 35.7, 41.1, 36.2, 37.7, 40.2, 41.4, 35.2, 40.6, 
    38.8, 41.5, 39, 44.1, 38.5, 43.1, 36.8, 37.5, 38.1, 41.1, 
    35.6, 40.2, 37, 39.7, 40.2, 40.6, 32.1, 40.7, 37.3, 39, 39.2, 
    36.6, 36, 37.8, 36, 41.5, 46.1, 50, 48.7, 50, 47.6, 46.5, 
    45.4, 46.7, 43.3, 46.8, 40.9, 49, 45.5, 48.4, 45.8, 49.3, 
    42, 49.2, 46.2, 48.7, 50.2, 45.1, 46.5, 46.3, 42.9, 46.1, 
    44.5, 47.8, 48.2, 50, 47.3, 42.8, 45.1, 59.6, 49.1, 48.4, 
    42.6, 44.4, 44, 48.7, 42.7, 49.6, 45.3, 49.6, 50.5, 43.6, 
    45.5, 50.5, 44.9, 45.2, 46.6, 48.5, 45.1, 50.1, 46.5, 45, 
    43.8, 45.5, 43.2, 50.4, 45.3, 46.2, 45.7, 54.3, 45.8, 49.8, 
    46.2, 49.5, 43.5, 50.7, 47.7, 46.4, 48.2, 46.5, 46.4, 48.6, 
    47.5, 51.1, 45.2, 45.2, 49.1, 52.5, 47.4, 50, 44.9, 50.8, 
    43.4, 51.3, 47.5, 52.1, 47.5, 52.2, 45.5, 49.5, 44.5, 50.8, 
    49.4, 46.9, 48.4, 51.1, 48.5, 55.9, 47.2, 49.1, 47.3, 46.8, 
    41.7, 53.4, 43.3, 48.1, 50.5, 49.8, 43.5, 51.5, 46.2, 55.1, 
    44.5, 48.8, 47.2, NA, 46.8, 50.4, 45.2, 49.9, 46.5, 50, 51.3, 
    45.4, 52.7, 45.2, 46.1, 51.3, 46, 51.3, 46.6, 51.7, 47, 52, 
    45.9, 50.5, 50.3, 58, 46.4, 49.2, 42.4, 48.5, 43.2, 50.6, 
    46.7, 52, 50.5, 49.5, 46.4, 52.8, 40.9, 54.2, 42.5, 51, 49.7, 
    47.5, 47.6, 52, 46.9, 53.5, 49, 46.2, 50.9, 45.5, 50.9, 50.8, 
    50.1, 49, 51.5, 49.8, 48.1, 51.4, 45.7, 50.7, 42.5, 52.2, 
    45.2, 49.3, 50.2, 45.6, 51.9, 46.8, 45.7, 55.8, 43.5, 49.6, 
    50.8, 50.2), bill_dep = c(18.7, 17.4, 18, NA, 19.3, 20.6, 
    17.8, 19.6, 18.1, 20.2, 17.1, 17.3, 17.6, 21.2, 21.1, 17.8, 
    19, 20.7, 18.4, 21.5, 18.3, 18.7, 19.2, 18.1, 17.2, 18.9, 
    18.6, 17.9, 18.6, 18.9, 16.7, 18.1, 17.8, 18.9, 17, 21.1, 
    20, 18.5, 19.3, 19.1, 18, 18.4, 18.5, 19.7, 16.9, 18.8, 19, 
    18.9, 17.9, 21.2, 17.7, 18.9, 17.9, 19.5, 18.1, 18.6, 17.5, 
    18.8, 16.6, 19.1, 16.9, 21.1, 17, 18.2, 17.1, 18, 16.2, 19.1, 
    16.6, 19.4, 19, 18.4, 17.2, 18.9, 17.5, 18.5, 16.8, 19.4, 
    16.1, 19.1, 17.2, 17.6, 18.8, 19.4, 17.8, 20.3, 19.5, 18.6, 
    19.2, 18.8, 18, 18.1, 17.1, 18.1, 17.3, 18.9, 18.6, 18.5, 
    16.1, 18.5, 17.9, 20, 16, 20, 18.6, 18.9, 17.2, 20, 17, 19, 
    16.5, 20.3, 17.7, 19.5, 20.7, 18.3, 17, 20.5, 17, 18.6, 17.2, 
    19.8, 17, 18.5, 15.9, 19, 17.6, 18.3, 17.1, 18, 17.9, 19.2, 
    18.5, 18.5, 17.6, 17.5, 17.5, 20.1, 16.5, 17.9, 17.1, 17.2, 
    15.5, 17, 16.8, 18.7, 18.6, 18.4, 17.8, 18.1, 17.1, 18.5, 
    13.2, 16.3, 14.1, 15.2, 14.5, 13.5, 14.6, 15.3, 13.4, 15.4, 
    13.7, 16.1, 13.7, 14.6, 14.6, 15.7, 13.5, 15.2, 14.5, 15.1, 
    14.3, 14.5, 14.5, 15.8, 13.1, 15.1, 14.3, 15, 14.3, 15.3, 
    15.3, 14.2, 14.5, 17, 14.8, 16.3, 13.7, 17.3, 13.6, 15.7, 
    13.7, 16, 13.7, 15, 15.9, 13.9, 13.9, 15.9, 13.3, 15.8, 14.2, 
    14.1, 14.4, 15, 14.4, 15.4, 13.9, 15, 14.5, 15.3, 13.8, 14.9, 
    13.9, 15.7, 14.2, 16.8, 14.4, 16.2, 14.2, 15, 15, 15.6, 15.6, 
    14.8, 15, 16, 14.2, 16.3, 13.8, 16.4, 14.5, 15.6, 14.6, 15.9, 
    13.8, 17.3, 14.4, 14.2, 14, 17, 15, 17.1, 14.5, 16.1, 14.7, 
    15.7, 15.8, 14.6, 14.4, 16.5, 15, 17, 15.5, 15, 13.8, 16.1, 
    14.7, 15.8, 14, 15.1, 15.2, 15.9, 15.2, 16.3, 14.1, 16, 15.7, 
    16.2, 13.7, NA, 14.3, 15.7, 14.8, 16.1, 17.9, 19.5, 19.2, 
    18.7, 19.8, 17.8, 18.2, 18.2, 18.9, 19.9, 17.8, 20.3, 17.3, 
    18.1, 17.1, 19.6, 20, 17.8, 18.6, 18.2, 17.3, 17.5, 16.6, 
    19.4, 17.9, 19, 18.4, 19, 17.8, 20, 16.6, 20.8, 16.7, 18.8, 
    18.6, 16.8, 18.3, 20.7, 16.6, 19.9, 19.5, 17.5, 19.1, 17, 
    17.9, 18.5, 17.9, 19.6, 18.7, 17.3, 16.4, 19, 17.3, 19.7, 
    17.3, 18.8, 16.6, 19.9, 18.8, 19.4, 19.5, 16.5, 17, 19.8, 
    18.1, 18.2, 19, 18.7), flipper_len = c(181L, 186L, 195L, 
    NA, 193L, 190L, 181L, 195L, 193L, 190L, 186L, 180L, 182L, 
    191L, 198L, 185L, 195L, 197L, 184L, 194L, 174L, 180L, 189L, 
    185L, 180L, 187L, 183L, 187L, 172L, 180L, 178L, 178L, 188L, 
    184L, 195L, 196L, 190L, 180L, 181L, 184L, 182L, 195L, 186L, 
    196L, 185L, 190L, 182L, 179L, 190L, 191L, 186L, 188L, 190L, 
    200L, 187L, 191L, 186L, 193L, 181L, 194L, 185L, 195L, 185L, 
    192L, 184L, 192L, 195L, 188L, 190L, 198L, 190L, 190L, 196L, 
    197L, 190L, 195L, 191L, 184L, 187L, 195L, 189L, 196L, 187L, 
    193L, 191L, 194L, 190L, 189L, 189L, 190L, 202L, 205L, 185L, 
    186L, 187L, 208L, 190L, 196L, 178L, 192L, 192L, 203L, 183L, 
    190L, 193L, 184L, 199L, 190L, 181L, 197L, 198L, 191L, 193L, 
    197L, 191L, 196L, 188L, 199L, 189L, 189L, 187L, 198L, 176L, 
    202L, 186L, 199L, 191L, 195L, 191L, 210L, 190L, 197L, 193L, 
    199L, 187L, 190L, 191L, 200L, 185L, 193L, 193L, 187L, 188L, 
    190L, 192L, 185L, 190L, 184L, 195L, 193L, 187L, 201L, 211L, 
    230L, 210L, 218L, 215L, 210L, 211L, 219L, 209L, 215L, 214L, 
    216L, 214L, 213L, 210L, 217L, 210L, 221L, 209L, 222L, 218L, 
    215L, 213L, 215L, 215L, 215L, 216L, 215L, 210L, 220L, 222L, 
    209L, 207L, 230L, 220L, 220L, 213L, 219L, 208L, 208L, 208L, 
    225L, 210L, 216L, 222L, 217L, 210L, 225L, 213L, 215L, 210L, 
    220L, 210L, 225L, 217L, 220L, 208L, 220L, 208L, 224L, 208L, 
    221L, 214L, 231L, 219L, 230L, 214L, 229L, 220L, 223L, 216L, 
    221L, 221L, 217L, 216L, 230L, 209L, 220L, 215L, 223L, 212L, 
    221L, 212L, 224L, 212L, 228L, 218L, 218L, 212L, 230L, 218L, 
    228L, 212L, 224L, 214L, 226L, 216L, 222L, 203L, 225L, 219L, 
    228L, 215L, 228L, 216L, 215L, 210L, 219L, 208L, 209L, 216L, 
    229L, 213L, 230L, 217L, 230L, 217L, 222L, 214L, NA, 215L, 
    222L, 212L, 213L, 192L, 196L, 193L, 188L, 197L, 198L, 178L, 
    197L, 195L, 198L, 193L, 194L, 185L, 201L, 190L, 201L, 197L, 
    181L, 190L, 195L, 181L, 191L, 187L, 193L, 195L, 197L, 200L, 
    200L, 191L, 205L, 187L, 201L, 187L, 203L, 195L, 199L, 195L, 
    210L, 192L, 205L, 210L, 187L, 196L, 196L, 196L, 201L, 190L, 
    212L, 187L, 198L, 199L, 201L, 193L, 203L, 187L, 197L, 191L, 
    203L, 202L, 194L, 206L, 189L, 195L, 207L, 202L, 193L, 210L, 
    198L), body_mass = c(3750L, 3800L, 3250L, NA, 3450L, 3650L, 
    3625L, 4675L, 3475L, 4250L, 3300L, 3700L, 3200L, 3800L, 4400L, 
    3700L, 3450L, 4500L, 3325L, 4200L, 3400L, 3600L, 3800L, 3950L, 
    3800L, 3800L, 3550L, 3200L, 3150L, 3950L, 3250L, 3900L, 3300L, 
    3900L, 3325L, 4150L, 3950L, 3550L, 3300L, 4650L, 3150L, 3900L, 
    3100L, 4400L, 3000L, 4600L, 3425L, 2975L, 3450L, 4150L, 3500L, 
    4300L, 3450L, 4050L, 2900L, 3700L, 3550L, 3800L, 2850L, 3750L, 
    3150L, 4400L, 3600L, 4050L, 2850L, 3950L, 3350L, 4100L, 3050L, 
    4450L, 3600L, 3900L, 3550L, 4150L, 3700L, 4250L, 3700L, 3900L, 
    3550L, 4000L, 3200L, 4700L, 3800L, 4200L, 3350L, 3550L, 3800L, 
    3500L, 3950L, 3600L, 3550L, 4300L, 3400L, 4450L, 3300L, 4300L, 
    3700L, 4350L, 2900L, 4100L, 3725L, 4725L, 3075L, 4250L, 2925L, 
    3550L, 3750L, 3900L, 3175L, 4775L, 3825L, 4600L, 3200L, 4275L, 
    3900L, 4075L, 2900L, 3775L, 3350L, 3325L, 3150L, 3500L, 3450L, 
    3875L, 3050L, 4000L, 3275L, 4300L, 3050L, 4000L, 3325L, 3500L, 
    3500L, 4475L, 3425L, 3900L, 3175L, 3975L, 3400L, 4250L, 3400L, 
    3475L, 3050L, 3725L, 3000L, 3650L, 4250L, 3475L, 3450L, 3750L, 
    3700L, 4000L, 4500L, 5700L, 4450L, 5700L, 5400L, 4550L, 4800L, 
    5200L, 4400L, 5150L, 4650L, 5550L, 4650L, 5850L, 4200L, 5850L, 
    4150L, 6300L, 4800L, 5350L, 5700L, 5000L, 4400L, 5050L, 5000L, 
    5100L, 4100L, 5650L, 4600L, 5550L, 5250L, 4700L, 5050L, 6050L, 
    5150L, 5400L, 4950L, 5250L, 4350L, 5350L, 3950L, 5700L, 4300L, 
    4750L, 5550L, 4900L, 4200L, 5400L, 5100L, 5300L, 4850L, 5300L, 
    4400L, 5000L, 4900L, 5050L, 4300L, 5000L, 4450L, 5550L, 4200L, 
    5300L, 4400L, 5650L, 4700L, 5700L, 4650L, 5800L, 4700L, 5550L, 
    4750L, 5000L, 5100L, 5200L, 4700L, 5800L, 4600L, 6000L, 4750L, 
    5950L, 4625L, 5450L, 4725L, 5350L, 4750L, 5600L, 4600L, 5300L, 
    4875L, 5550L, 4950L, 5400L, 4750L, 5650L, 4850L, 5200L, 4925L, 
    4875L, 4625L, 5250L, 4850L, 5600L, 4975L, 5500L, 4725L, 5500L, 
    4700L, 5500L, 4575L, 5500L, 5000L, 5950L, 4650L, 5500L, 4375L, 
    5850L, 4875L, 6000L, 4925L, NA, 4850L, 5750L, 5200L, 5400L, 
    3500L, 3900L, 3650L, 3525L, 3725L, 3950L, 3250L, 3750L, 4150L, 
    3700L, 3800L, 3775L, 3700L, 4050L, 3575L, 4050L, 3300L, 3700L, 
    3450L, 4400L, 3600L, 3400L, 2900L, 3800L, 3300L, 4150L, 3400L, 
    3800L, 3700L, 4550L, 3200L, 4300L, 3350L, 4100L, 3600L, 3900L, 
    3850L, 4800L, 2700L, 4500L, 3950L, 3650L, 3550L, 3500L, 3675L, 
    4450L, 3400L, 4300L, 3250L, 3675L, 3325L, 3950L, 3600L, 4050L, 
    3350L, 3450L, 3250L, 4050L, 3800L, 3525L, 3950L, 3650L, 3650L, 
    4000L, 3400L, 3775L, 4100L, 3775L), sex = structure(c(2L, 
    1L, 1L, NA, 1L, 2L, 1L, 2L, NA, NA, NA, NA, 1L, 2L, 2L, 1L, 
    1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 2L, 1L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 
    2L, NA, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 
    1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 2L, 1L, 1L, 
    2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 
    1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 
    1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 
    1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, NA, 2L, 1L, 
    2L, 2L, 1L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 
    2L, 1L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 1L, 2L, NA, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 
    1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 1L, 2L, 
    NA, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, NA, 2L, 1L, 
    NA, 1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 2L, 1L, 1L, 2L, 1L, 2L, 
    1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 
    2L, 1L, 2L, 1L, 2L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 
    2L, 1L, 2L, 1L, 1L, 2L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 2L, 1L, 
    2L, 1L, 2L, 2L, 1L, 2L, 1L, 1L, 2L, 1L, 2L, 2L, 1L), levels = c("female", 
    "male"), class = "factor"), year = c(2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 2007L, 
    2007L, 2007L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 2008L, 
    2008L, 2008L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 
    2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L, 2009L)), row.names = c(NA, 
-344L), class = "data.frame")


penguin_coef_explain_app <- function() {
  ui <- page_sidebar(
    sidebar = sidebar(
      radioButtons("response", "Response",
                         choiceNames = c("body_mass_g", "bill length_mm", "bill depth mm", "flipper length mm"),
                         choiceValues = c(
                           "body_mass",
                           "bill_len",
                           "bill_dep",
                           "flipper_len"
                         ),
                   selected = "body_mass"
      ),
      checkboxGroupInput("pred", "Predictor",
                         choiceValues = c("species", "sex", "interaction"),
                         choiceNames = c(
                           "species",
                           "sex",
                           "interaction"
                         )
      )


    ),
    card(
      textOutput("formula"),
      fill = FALSE
    ),
    card(
      card_header("Coefficients"),
      tableOutput("coef_table")
    ),
    card(
      plotOutput("plot")
    ),
    tags$head(tags$style("#coef_table td{
                     position:relative;
                     };

                     ")),
  )



  server <- function(input, output, session) {
    data <-  penguins |> na.omit()
    data <- data[order(data$species), ]
    data <- data[order(data$sex), ]



    form2 <- reactive({
      form <- paste(input$response,"~")

      if ("interaction" %in% input$pred) {
        paste(form, "species * sex")
      } else if ("species" %in% input$pred & "sex" %in% input$pred) {
        paste(form, "species + sex")
      } else if ("species" %in% input$pred) {
        paste(form, "species")
      } else if ("sex" %in% input$pred) {
        paste(form, "sex")
      } else {
        paste(form, "1")
      }
    })

    observe({
      if ("interaction" %in% input$pred) {
        updateCheckboxGroupInput(session, "pred",
                                 selected = c("species", "sex", "interaction")
        )
      }
    })

    model <- reactive({
      lm(form2(), data = data)
    })

    coefs <- reactive({
      coef(model())
    })

    coef_colours <- reactive({
      c(
        `(Intercept)` = "skyblue",
        speciesChinstrap = "pink",
        speciesGentoo = "red",


        sexmale = "green",
        `speciesChinstrap:sexmale` = "brown",
        `speciesGentoo:sexmale` = "orange"

      )[names(coefs())]
    })

    coef_table <- reactive({
      c1 <- '<div style="width: 100%; height: 100%; z-index: 0; background-color: '
      c2 <- '; position:absolute; top: 0; left: 0; padding:5px;">\n<span>'
      c3 <- "</span></div>"

      tab <- data.frame(
        Beta = paste0(c1, coef_colours(), c2, "\u03B2", seq_along(coefs()), c3),
        Coefficent = names(coefs()),
        Estimate = coefs()
      )
      tab
    })


    output$formula <- renderText(
      paste0("lm(", form2(), ", data = penguins)")
      )
    output$coef_table <- renderTable(
      coef_table(),
      sanitize.text.function = function(x) x
    )
    output$plot <- renderPlot({
      par(par_list)
      set.seed(1)
      f <- as.formula(form2())
      fc <- as.character(f)
      ylim <- c(0, max(data[, input$response]))
      if (fc[3] == "1") {
        stripchart(data[,input$response],
                   method = "jitter", jitter = 0.1,
                   vertical = TRUE, pch = 1, ylim = ylim,
                   ylab = fc[2]
                   )
        axis(side = 1, at = 1, labels = "All penguins")
      } else {
        spp <- levels(data$species)
        sex <- levels(data$sex)
        group_names <-
           if ("species" %in% input$pred & "sex" %in% input$pred) {
          paste("\n", rep(spp, times = length(sex)), rep(sex, each = length(spp)), sep = "\n")
          } else if ("species" %in% input$pred) {
            spp
          } else if ("sex" %in% input$pred) {
            sex
          } else {
            1
          }

        stripchart(f,
                   data = data, method = "jitter", jitter = 0.1,
                   vertical = TRUE, pch = 1, ylim = ylim,
                   group.names = group_names
        )
      }

      cols <- c("species", "sex")[c(grepl("species", fc[3]), grepl("sex", fc[3]))]
      if (length(cols) == 0) {
        cols <- "species"
      }
      pred <- predict(model(), newdata = unique(data[, cols, drop = FALSE]))
      points(seq_along(pred), pred, col = "#832424", pch = 16, cex = 4)

      # add arrows for betas
      lwd <- 3
      xs <- seq_along(pred) - 0.2
      # b0
      arrows(xs, rep(0, length(pred)), xs, rep(coefs()[1], length(pred)),
             col = coef_colours()[1], lwd = lwd, length = 0.1
      )

      # species main effect
      pos <- 2 - 0.2 # x position
      if ("speciesChinstrap" %in% names(coefs())) {
        arrows(pos, coefs()[1], pos, coefs()[1] + coefs()["speciesChinstrap"],
               col = coef_colours()["speciesChinstrap"], lwd = lwd, length = 0.1
        )

        pos <- pos + 1 # move to next position
        arrows(pos, coefs()[1], pos, coefs()[1] + coefs()["speciesGentoo"],
               col = coef_colours()["speciesGentoo"], lwd = lwd, length = 0.1
        )

        pos <- pos + 1 # move to next position
      }

      if ("sexmale" %in% names(coefs())) {
        arrows(pos, coefs()[1], pos, coefs()[1] + coefs()["sexmale"],
               col = coef_colours()["sexmale"], lwd = lwd, length = 0.1
        )
        pos <- pos + 1
      }

      if (all(c("speciesChinstrap", "sexmale") %in% names(coefs()))) {
        #chinstraps
        arrows(pos, coefs()[1], pos, coefs()[1] + coefs()["speciesChinstrap"],
               col = coef_colours()["speciesChinstrap"], lwd = lwd, length = 0.1
        )

        arrows(pos,
               coefs()[1] + coefs()["speciesChinstrap"],
               pos,
               coefs()[1] + coefs()["speciesChinstrap"] + coefs()["sexmale"],
               col = coef_colours()["sexmale"],
               lwd = lwd, length = 0.1
        )

        if ("speciesChinstrap:sexmale" %in% names(coefs())) { # interaction
          arrows(pos,
                 coefs()[1] + coefs()["speciesChinstrap"] + coefs()["sexmale"],
                 pos,
                 coefs()[1] + coefs()["speciesChinstrap"] +
                   coefs()["sexmale"] +
                   coefs()["speciesChinstrap:sexmale"],
                 col = coef_colours()["speciesChinstrap:sexmale"],
                 lwd = lwd, length = 0.1
          )
        }

        # gentoo
        pos <- pos + 1
        arrows(pos, coefs()[1], pos, coefs()[1] + coefs()["speciesGentoo"],
               col = coef_colours()["speciesGentoo"], lwd = lwd, length = 0.1
        )

        arrows(pos,
               coefs()[1] + coefs()["speciesGentoo"],
               pos,
               coefs()[1] + coefs()["speciesGentoo"] + coefs()["sexmale"],
               col = coef_colours()["sexmale"],
               lwd = lwd, length = 0.1
        )

        if ("speciesGentoo:sexmale" %in% names(coefs())) { # interaction
          arrows(pos,
                 coefs()[1] + coefs()["speciesGentoo"] + coefs()["sexmale"],
                 pos,
                 coefs()[1] + coefs()["speciesGentoo"] +
                   coefs()["sexmale"] +
                   coefs()["speciesGentoo:sexmale"],
                 col = coef_colours()["speciesGentoo:sexmale"],
                 lwd = lwd, length = 0.1
          )
        }
      }
    })
  }

  shinyApp(ui, server)
}



par_list <- list(
  mar = c(2.2, 2.2, 0.5, 0.5),
  cex = 1.5,
  tcl = -0.1,
  mgp = c(1.2, 0.2, 0)
)

penguin_coef_explain_app()

Interaction between continuous and categorical predictors

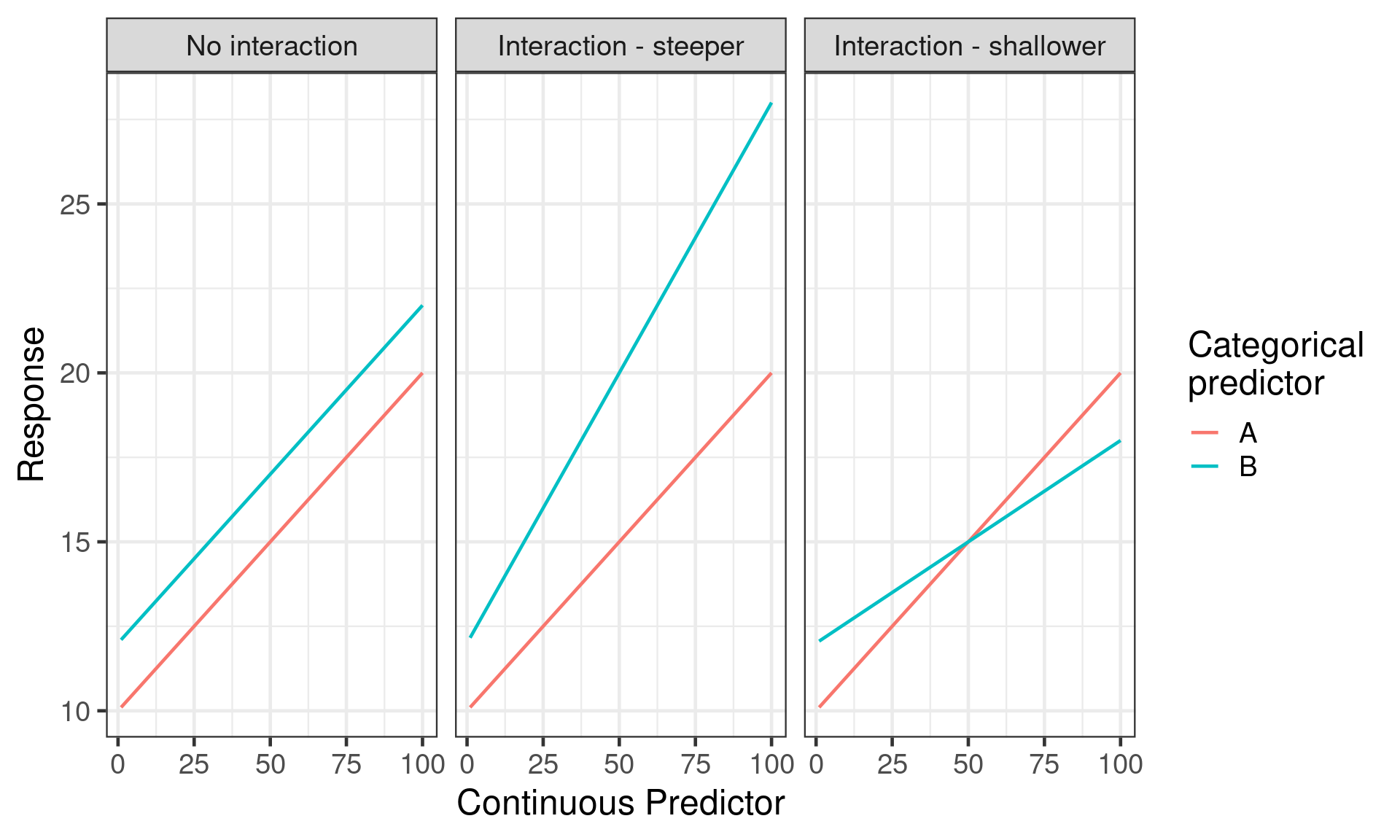
mod_interact <- lm(bill_length_mm ~ sex * flipper_length_mm, data = adelie)
summary(mod_interact)

Call:
lm(formula = bill_length_mm ~ sex * flipper_length_mm, data = adelie)

Residuals:
   Min     1Q Median     3Q    Max 
-6.395 -1.329  0.029  1.427  5.438 

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
(Intercept)                39.7935     8.3528    4.76  4.6e-06 ***
sexmale                   -20.2163    11.0648   -1.83    0.070 .  
flipper_length_mm          -0.0135     0.0445   -0.30    0.762    
sexmale:flipper_length_mm   0.1217     0.0583    2.09    0.039 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.11 on 142 degrees of freedom
Multiple R-squared:  0.385, Adjusted R-squared:  0.372 
F-statistic: 29.6 on 3 and 142 DF,  p-value: 6.43e-15

Interaction between two continuous predictors

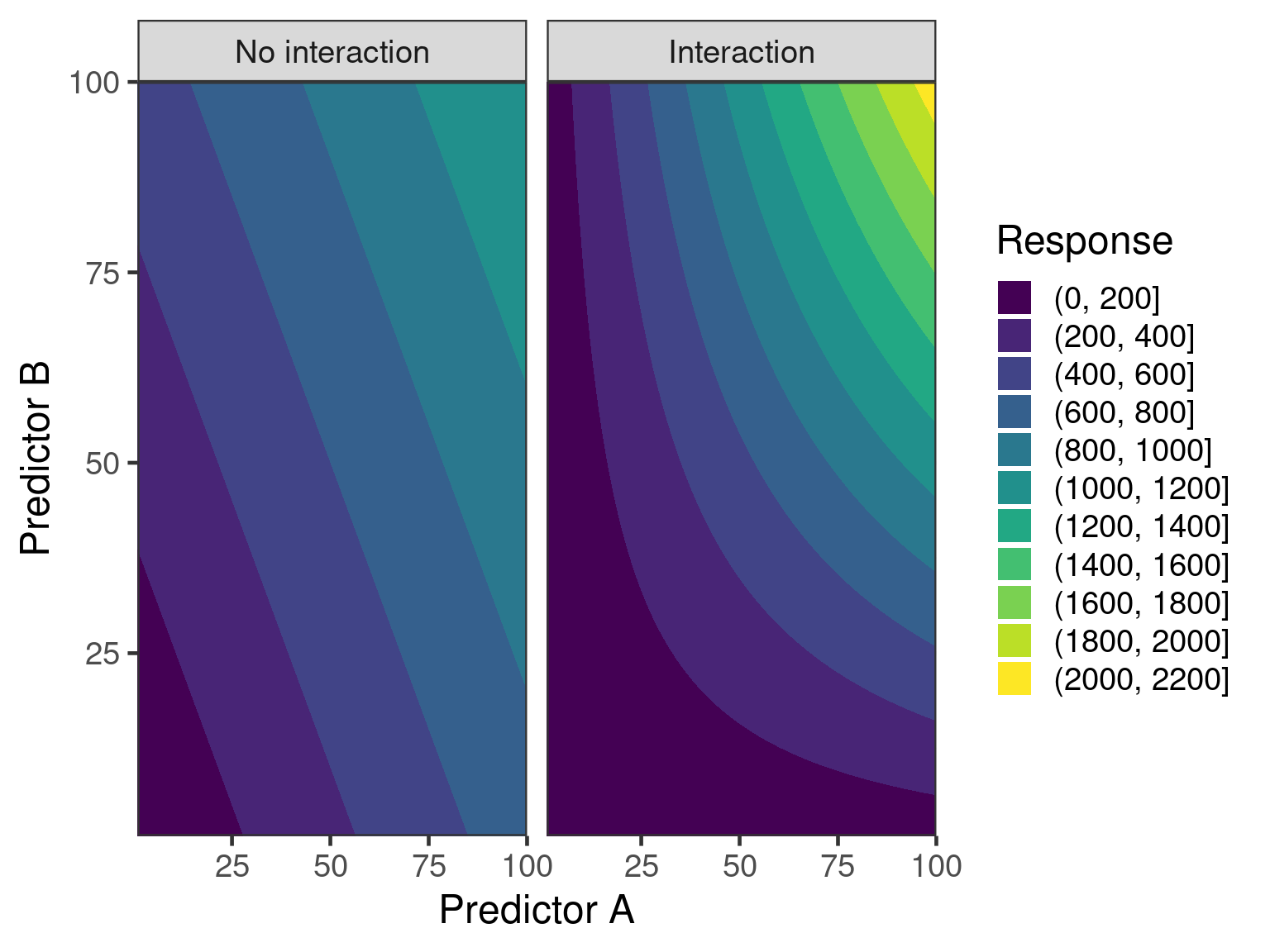
mod <- lm(flipper_length_mm ~ body_mass_g * bill_length_mm, data = adelie)
summary(mod)

Call:
lm(formula = flipper_length_mm ~ body_mass_g * bill_length_mm, 
    data = adelie)

Residuals:
    Min      1Q  Median      3Q     Max 
-14.653  -3.101  -0.003   3.369  16.585 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 2.04e+02   5.72e+01    3.58  0.00048 ***
body_mass_g                -6.63e-03   1.52e-02   -0.44  0.66330    
bill_length_mm             -9.19e-01   1.48e+00   -0.62  0.53531    
body_mass_g:bill_length_mm  3.17e-04   3.89e-04    0.82  0.41546    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.79 on 142 degrees of freedom
Multiple R-squared:  0.229, Adjusted R-squared:  0.212 
F-statistic:   14 on 3 and 142 DF,  p-value: 4.62e-08

Power needed for interactions

  • Main effect = \(\bar{y_1}\) - \(\bar{y_2}\)
  • Interaction = (\(\bar{y_1}\) - \(\bar{y_2}\)) - (\(\bar{y_3}\) - \(\bar{y_4}\))
set.seed(42)
sigma <- 10
n <- 1000
random <- tibble(
  x = sample(c("A", "B"), n, replace = TRUE),
  z = sample(factor(1:2), n, replace = TRUE),
  y = rnorm(n, mean = 0, sd = sigma)
)

lm(y ~ x * z, data = random) |> tidy()
# A tibble: 4 × 5
  term        estimate std.error statistic p.value
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    0.281     0.615     0.457  0.647 
2 xB            -1.90      0.864    -2.20   0.0280
3 z2             0.759     0.880     0.863  0.388 
4 xB:z2          1.06      1.24      0.849  0.396

Formula for interactions

y ~ x + z + x:z

y ~ x * z

y ~ (x + z)^2

Use y ~ x + I(x^2) to get a quadratic. Or y ~ poly(x, 2)

mod1 <- lm(flipper_length_mm ~ species + sex + species:sex, data = penguins)
mod2 <- lm(flipper_length_mm ~ species * sex, data = penguins)
mod3 <- lm(flipper_length_mm ~ (species + sex)^2, data = penguins)

coef(mod1)
             (Intercept)         speciesChinstrap            speciesGentoo 
                 187.795                    3.941                   24.912 
                 sexmale speciesChinstrap:sexmale    speciesGentoo:sexmale 
                   4.616                    3.560                    4.218 
coef(mod2)
             (Intercept)         speciesChinstrap            speciesGentoo 
                 187.795                    3.941                   24.912 
                 sexmale speciesChinstrap:sexmale    speciesGentoo:sexmale 
                   4.616                    3.560                    4.218 
coef(mod3)
             (Intercept)         speciesChinstrap            speciesGentoo 
                 187.795                    3.941                   24.912 
                 sexmale speciesChinstrap:sexmale    speciesGentoo:sexmale 
                   4.616                    3.560                    4.218

Model Selection

You want to the best model!

The best model for what?

  • Exploratory data analysis
  • Inference (hypothesis testing)
  • Predictions

Exploratory analysis

  • Consider all plausible models
  • P-values not meaningful
  • High type I error rate
  • Suggest hypotheses for hypothesis testing with independent data

The more biology you include in the model, the better

Automatic model selection

Last resort - many problems and biases

  • Forward selection

  • Backwards selection

  • All possible models

library(MuMIn)
library(conflicted)
conflict_prefer("filter", "dplyr")
conflict_prefer("select", "dplyr")

penguins2 <- penguins |>
  drop_na() |>
  select(-year)
full <- lm(body_mass_g ~ ., data = penguins2, na.action = "na.fail")

AIC

AIC Akaike information criterion \(2k - 2 \times log(likelihood)\)
(k the number of parameters)

Measure of how well the model fit the data

Penalised for model complexity

AICc correction for small sample sizes

AIC weights - probability model is best of those tested

dredge(full) |> gt::gt()
(Intercept) bill_depth_mm bill_length_mm flipper_length_mm island sex species df logLik AICc delta weight
-1461.0 67.22 18.204 15.95 NA + + 8 -2354 4724 0.000 7.682e-01
-1500.0 67.58 18.189 16.24 + + + 10 -2354 4728 3.543 1.307e-01
-1211.5 74.38 NA 17.54 NA + + 7 -2357 4729 4.537 7.948e-02
-1245.4 74.51 NA 17.85 + + + 9 -2357 4732 8.027 1.388e-02
-759.1 NA 21.633 17.85 NA + + 7 -2360 4734 9.536 6.526e-03
-785.6 NA 21.528 18.14 + + + 9 -2359 4738 13.153 1.070e-03
-365.8 NA NA 20.02 NA + + 6 -2364 4741 16.649 1.863e-04
-390.0 NA NA 20.32 + + + 8 -2364 4745 20.118 3.287e-05
844.0 87.93 26.537 NA NA + + 7 -2369 4752 27.263 9.232e-07
829.8 88.33 26.664 NA + + + 9 -2369 4756 31.392 1.172e-07
1577.0 102.04 NA NA NA + + 6 -2375 4763 38.571 3.236e-09
1576.2 102.15 NA NA + + + 8 -2375 4767 42.751 4.000e-10
2169.3 NA 32.537 NA NA + + 6 -2378 4768 43.901 2.252e-10
2167.9 NA 32.535 NA + + + 8 -2378 4772 48.086 2.778e-11
-4282.1 141.77 39.718 20.23 NA NA + 7 -2385 4784 59.631 8.643e-14
3372.4 NA NA NA NA + + 5 -2388 4786 61.394 3.580e-14
-4324.0 141.82 39.599 20.58 + NA + 9 -2384 4786 62.049 2.580e-14
3375.8 NA NA NA + + + 7 -2388 4790 65.442 4.731e-15
-2219.3 -50.03 NA 35.69 + + NA 7 -2397 4807 82.977 7.364e-19
-2115.6 -50.34 6.052 33.94 + + NA 8 -2396 4808 83.566 5.488e-19
-4484.7 181.95 NA 25.53 NA NA + 6 -2400 4811 86.962 1.004e-19
-4524.1 181.54 NA 25.95 + NA + 8 -2399 4814 89.247 3.204e-20
-3720.1 NA NA 39.30 + + NA 6 -2401 4815 90.409 1.792e-20
-3629.6 NA 5.808 37.64 + + NA 7 -2401 4816 91.143 1.242e-20
-1709.5 180.78 54.061 NA NA NA + 6 -2405 4822 97.444 5.318e-22
-1735.5 181.30 54.252 NA + NA + 8 -2404 4825 100.777 1.005e-22
-3864.1 NA 60.117 27.54 NA NA + 6 -2411 4833 109.078 1.583e-24
-2246.8 -86.95 NA 38.19 NA + NA 5 -2412 4834 109.703 1.158e-24
-2288.5 -86.09 -2.329 38.83 NA + NA 6 -2412 4836 111.527 4.653e-25
-3902.9 NA 59.868 27.96 + NA + 8 -2410 4836 111.692 4.284e-25
-5410.3 NA NA 46.98 NA + NA 4 -2427 4863 138.223 7.424e-31
-5433.5 NA -5.201 48.21 NA + NA 5 -2427 4864 139.128 4.723e-31
-1000.8 256.55 NA NA NA NA + 5 -2431 4871 146.983 9.299e-33
-1014.6 257.16 NA NA + NA + 7 -2430 4875 150.703 1.448e-33
-5707.1 51.24 13.748 42.90 + NA NA 7 -2438 4891 166.751 4.741e-37
-6114.7 56.67 NA 47.40 + NA NA 6 -2441 4895 170.817 6.209e-38
-4013.2 NA NA 40.61 NA NA + 5 -2443 4895 171.067 5.478e-38
-4047.8 NA NA 41.09 + NA + 7 -2442 4897 173.113 1.970e-38
200.5 NA 90.298 NA NA NA + 5 -2444 4899 174.468 1.001e-38
-4355.0 NA 16.883 39.66 + NA NA 6 -2445 4902 177.784 1.906e-39
182.0 NA 90.510 NA + NA + 7 -2444 4903 178.295 1.477e-39
-4687.9 NA NA 44.89 + NA NA 5 -2450 4909 184.809 5.685e-41
-6537.6 19.88 NA 51.77 NA NA NA 4 -2460 4928 203.674 4.552e-45
-5872.1 NA NA 50.15 NA NA NA 3 -2461 4928 203.836 4.198e-45
-5836.3 NA 4.959 48.89 NA NA NA 4 -2461 4929 204.973 2.377e-45
-6445.5 17.84 3.293 50.76 NA NA NA 5 -2460 4930 205.355 1.965e-45
4784.5 -155.12 44.769 NA + + NA 7 -2470 4955 230.236 7.767e-51
1747.4 NA 60.616 NA + + NA 6 -2505 5022 297.540 1.886e-65
6551.4 -257.31 36.519 NA NA + NA 5 -2507 5023 299.035 8.929e-66
7580.2 -211.52 NA NA + + NA 6 -2506 5024 299.241 8.057e-66
3706.2 NA NA NA NA NA + 4 -2513 5035 310.285 3.221e-68
3709.7 NA NA NA + NA + 6 -2513 5039 314.411 4.093e-69
8779.1 -299.34 NA NA NA + NA 4 -2529 5066 341.864 4.474e-75
1697.5 -26.23 76.000 NA + NA NA 6 -2537 5086 361.234 2.782e-79
1239.3 NA 76.905 NA + NA NA 5 -2538 5086 361.346 2.632e-79
4375.8 NA NA NA + + NA 5 -2562 5133 409.061 1.145e-89
3413.5 -145.51 74.813 NA NA NA NA 4 -2595 5199 474.205 8.187e-104
746.1 NA 74.025 NA NA + NA 4 -2614 5236 512.010 5.056e-112
5590.3 -54.76 NA NA + NA NA 5 -2615 5240 516.032 6.767e-113
4719.2 NA NA NA + NA NA 4 -2618 5244 519.963 9.482e-114
388.8 NA 86.792 NA NA NA NA 3 -2629 5264 539.833 4.594e-118
7520.0 -193.01 NA NA NA NA NA 3 -2658 5322 598.047 1.050e-130
3862.3 NA NA NA NA + NA 3 -2667 5340 615.648 1.582e-134
4207.1 NA NA NA NA NA NA 2 -2700 5404 679.945 1.727e-148

Inference

Test small number of a priori hypothesis.

Use anova() to compare nested models

H0 there is no interaction between sex and species for predicting body mass

mod1 <- lm(body_mass_g ~ species + sex, data = penguins)
mod2 <- lm(body_mass_g ~ species * sex, data = penguins)
anova(mod1, mod2)
Analysis of Variance Table

Model 1: body_mass_g ~ species + sex
Model 2: body_mass_g ~ species * sex
  Res.Df      RSS Df Sum of Sq    F Pr(>F)    
1    329 32979185                             
2    327 31302628  2   1676557 8.76  2e-04 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

car::Anova vs anova

mod2 <- lm(body_mass_g ~ species + sex, data = penguins)
mod3 <- lm(body_mass_g ~ sex + species, data = penguins)
  • anova() - tests terms sequentially - Anova type I
  • car::Anova() - marginal test - Anova type II
anova(mod2)
Analysis of Variance Table

Response: body_mass_g
           Df   Sum Sq  Mean Sq F value Pr(>F)    
species     2 1.45e+08 72595110     724 <2e-16 ***
sex         1 3.71e+07 37090262     370 <2e-16 ***
Residuals 329 3.30e+07   100241                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mod3)
Analysis of Variance Table

Response: body_mass_g
           Df   Sum Sq  Mean Sq F value Pr(>F)    
sex         1 3.89e+07 38878897     388 <2e-16 ***
species     2 1.43e+08 71700792     715 <2e-16 ***
Residuals 329 3.30e+07   100241                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
car::Anova(mod2)
Anova Table (Type II tests)

Response: body_mass_g
            Sum Sq  Df F value Pr(>F)    
species   1.43e+08   2     715 <2e-16 ***
sex       3.71e+07   1     370 <2e-16 ***
Residuals 3.30e+07 329                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
car::Anova(mod3)
Anova Table (Type II tests)

Response: body_mass_g
            Sum Sq  Df F value Pr(>F)    
sex       3.71e+07   1     370 <2e-16 ***
species   1.43e+08   2     715 <2e-16 ***
Residuals 3.30e+07 329                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Multicollinearity

  • Two or more predictor variables in a multiple regression model are highly correlated. Example: pH and calcium
  • Coefficient estimates are unstable
    • erratic change in response to small changes in the model or the data.
  • Solve by having lots of data
col <- performance::check_collinearity(full)
col
# Check for Multicollinearity

Low Correlation

   Term  VIF     VIF 95% CI adj. VIF Tolerance Tolerance 95% CI
 island 3.73 [ 3.14,  4.49]     1.39      0.27     [0.22, 0.32]
    sex 2.33 [ 2.00,  2.77]     1.53      0.43     [0.36, 0.50]

Moderate Correlation

              Term  VIF     VIF 95% CI adj. VIF Tolerance Tolerance 95% CI
    bill_length_mm 6.10 [ 5.06,  7.40]     2.47      0.16     [0.14, 0.20]
     bill_depth_mm 6.10 [ 5.06,  7.41]     2.47      0.16     [0.14, 0.20]
 flipper_length_mm 6.80 [ 5.63,  8.26]     2.61      0.15     [0.12, 0.18]

High Correlation

    Term   VIF     VIF 95% CI adj. VIF Tolerance Tolerance 95% CI
 species 63.52 [51.73, 78.06]     2.82      0.02     [0.01, 0.02]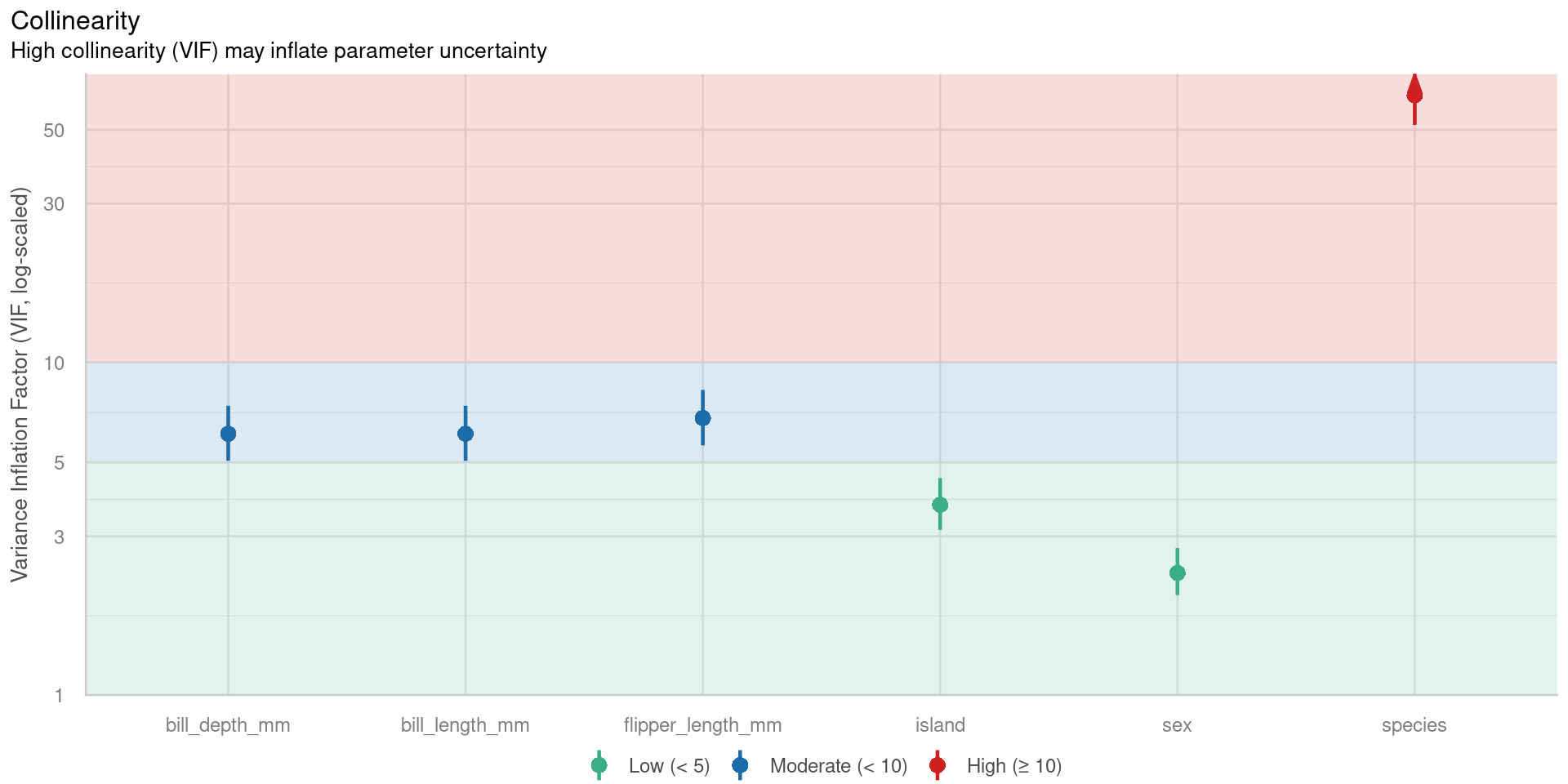
plot(col)

Autocorrelation

Linear models assume residuals are independent

If data are spatially or temporally structured, residuals may be correlated.

Positive autocorrelation

  • confidence intervals are too narrow
  • increases risk of false positive (Type I error)

Luteinising Hormone concentration

Code 
library(ggfortify)

lh <- fortify(lh) |>
  mutate(time = Index * 10) |>
  rename(concentration = Data)

mod_lh <- lm(concentration ~ time, data = lh)

augment(mod_lh, interval = "confidence") |>
  ggplot(aes(x = time, y = concentration)) +
  geom_line() +
  geom_point() +
  geom_ribbon(aes(ymin = .lower, ymax = .upper), alpha = 0.2, fill = "#ee5050") +
  geom_line(aes(y = .fitted), colour = "#ee5050") +
  labs(x = "Time, minutes", y = "Hormone concentration")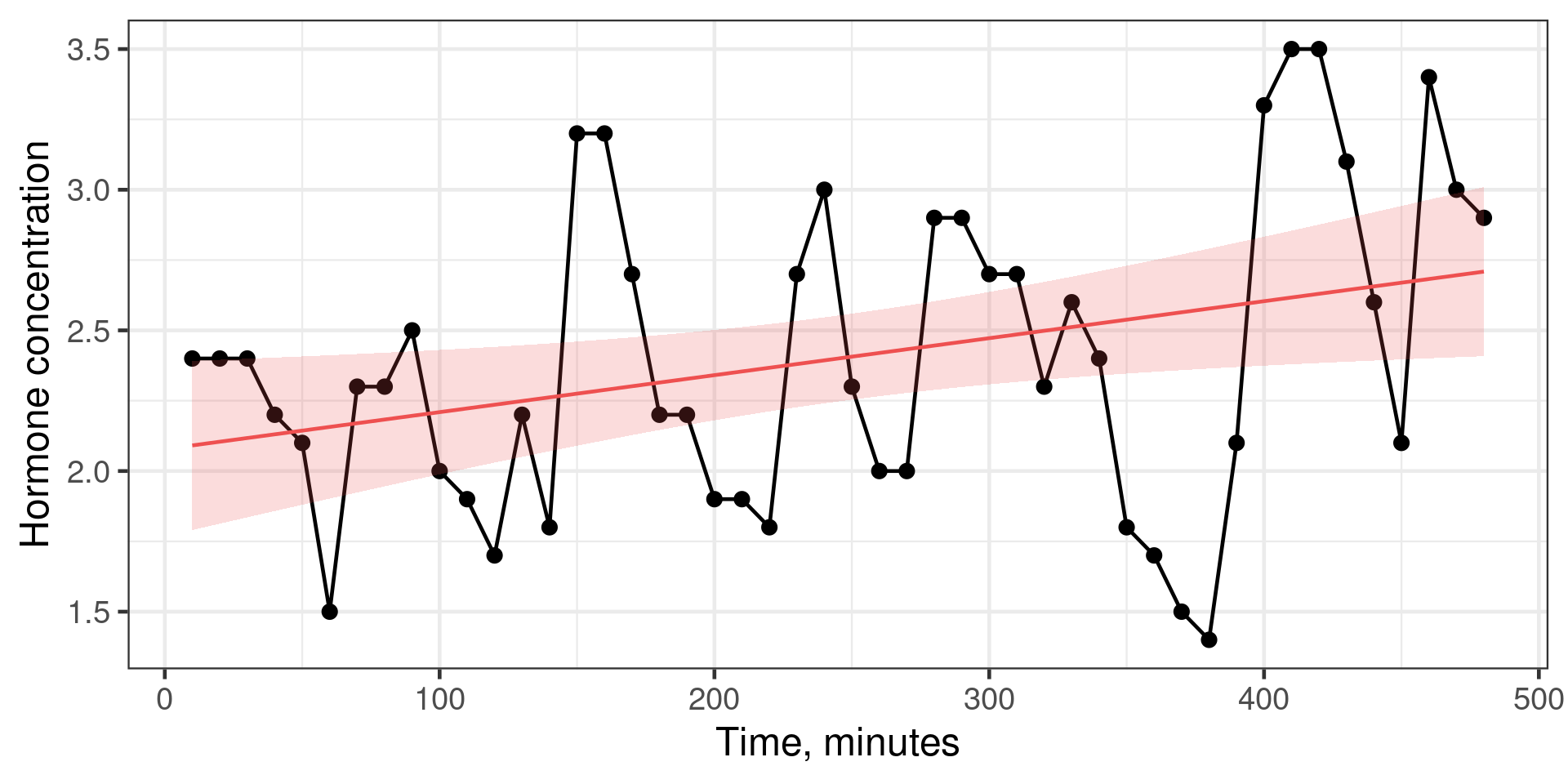

Detecting autocorrelation

For time series with equally-spaced observations, use autocorrelation function (ACF)

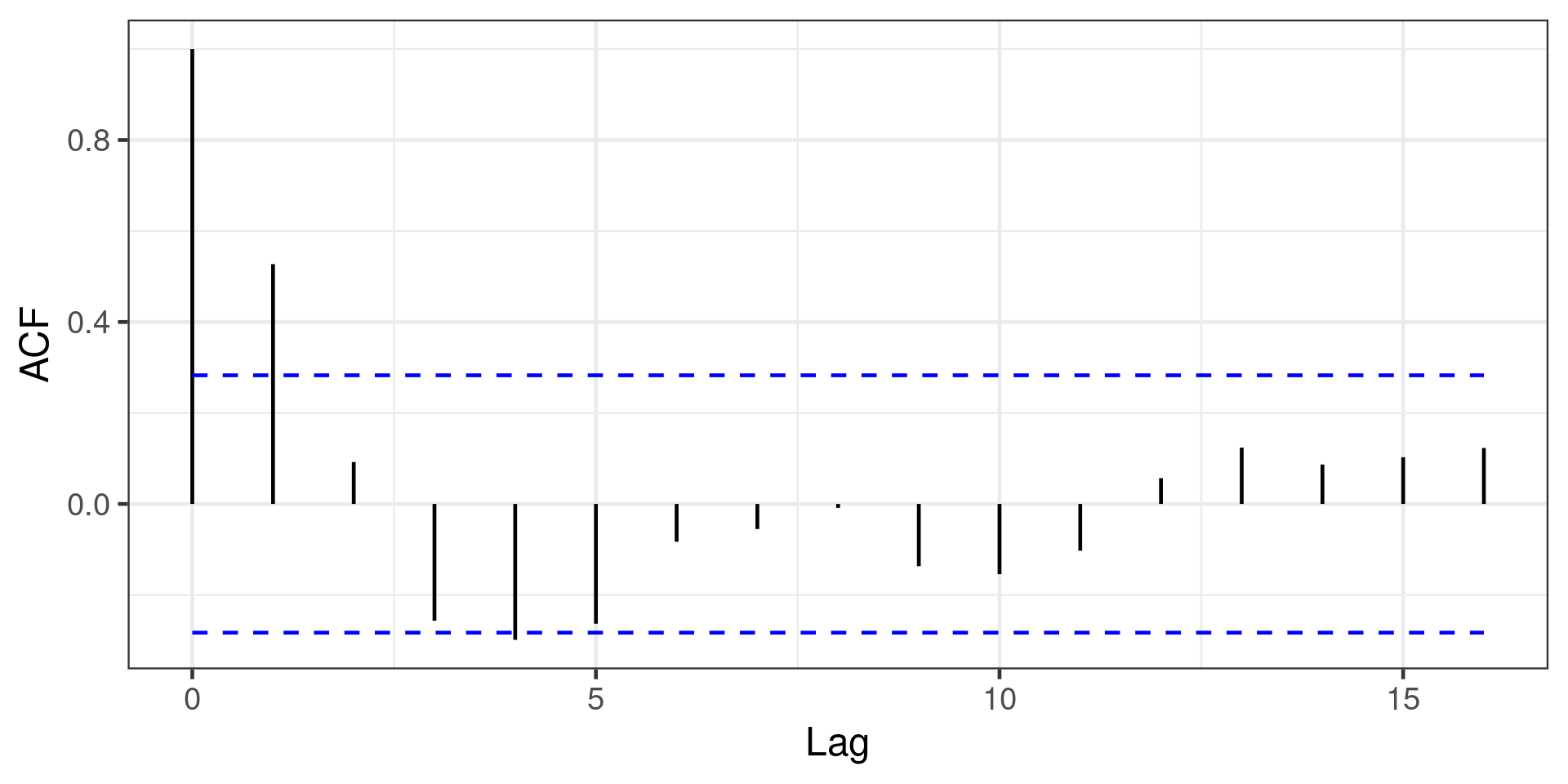
autoplot(acf(mod_lh$residuals, plot = FALSE))

Detecting autocorrelation

Tests for equally-spaced observations

Durbin-Watson test

performance::check_autocorrelation(mod_lh)
Warning: Autocorrelated residuals detected (p < .001).

Other methods for spatial data and non-equally spaced data

Solution - use a model that accounts for autocorrelation

  • generalised least squares (nlme::gls())

Reporting regression results - tables

Make a table - estimates, confidence intervals, p-values

Can calculate confidence intervals with broom::tidy() and format output

library(gt)
tidy(mod_mult, conf.int = TRUE) |>
  select(term, estimate, conf.low, conf.high, p.value) |>
  mutate(p.value = format.pval(p.value, eps = 0.001)) |>
  gt() |>
  fmt_number(
    columns = c(estimate, conf.low, conf.high),
    decimals = 4
  )
term estimate conf.low conf.high p.value
(Intercept) −3.4367 −12.4466 5.5732 0.45
body_mass_g 0.0007 −0.0005 0.0018 0.24
flipper_length_mm 0.2219 0.1582 0.2855 <0.001

gtsummary

Or make table with gtsummary

library(gtsummary)
tbl <- tbl_regression(mod_mult,
  label = list(
    body_mass_g = "Body mass g",
    flipper_length_mm = "Flipper length mm"
  ),
  estimate_fun = label_style_sigfig(digits = 4)
)
tbl
Characteristic Beta 95% CI p-value
Body mass g 0.0007 -0.0005, 0.0018 0.2
Flipper length mm 0.2219 0.1582, 0.2855 <0.001
Abbreviation: CI = Confidence Interval

Reporting regression results - inline

Can extract values directly from regression .

  • estimate
  • confidence intervals
  • p-value, degrees of freedom, statistic
Longer flipper length is associated with longer bill length 
(estimate = `r round(coef(mod_mult)["flipper_length_mm"], 2)` mm/mm, 
95% CI = `r round(confint(mod_mult)["flipper_length_mm", ], 2)` 
p = `r format.pval(tidy(mod_mult) |> filter(term == "flipper_length_mm") |> select("p.value"), eps = 0.001)`).

Longer flipper length is associated with longer bill length (estimate = 0.22 mm/mm, 95% CI = 0.16, 0.29 p = <0.001).

Also function inline_text() from gtsummary

See APA guide for reporting statistics